为了解某班学生关注NBA是否与性别有关，对本班48人进行了问卷调查得到如下的列联表：
| |
关注NBA |
不关注NBA |
合 计 |
| 男 生 |
|
6 |
|
| 女 生 |
10 |
|
|
| 合 计 |
|
|
48 |
已知在全班48人中随机抽取1人，抽到关注NBA的学生的概率为2/3
⑴请将上面列连表补充完整，并判断是否有
的把握认为关注NBA与性别有关？
⑵现从女生中抽取2人进一步调查，设其中关注NBA的女生人数为X，求X的分布列与数学期望。
附：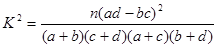
，其中 
 |
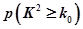0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
 |
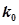2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
满足：
令
表示成
的不含
（即写出
的解析式），
时，求函数
的定义域为
，
的定义域为
。
，求
、
的取值范围。
，求函数
的值域.
的解集为
，求不等式
的解集。