求下列曲线的标准方程:
(1)两个焦点的坐标分别是 ,且双曲线过点
,且双曲线过点 ,求双曲线的标准方程;
,求双曲线的标准方程;
(2)求以原点为顶点,以坐标轴为对称轴,且焦点在直线 上的抛物线的标准方程.
上的抛物线的标准方程.
对于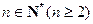 ,定义一个如下数阵:
,定义一个如下数阵: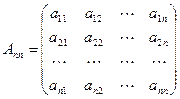
其中对任意的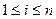 ,
, ,当
,当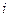 能整除
能整除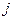 时,
时,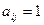 ;当
;当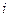 不能整除
不能整除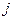 时,
时,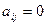 .
.
(Ⅰ)当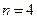 时,试写出数阵
时,试写出数阵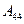 ;
;
(Ⅱ)设 .若
.若 表示不超过
表示不超过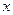 的最大整数,
的最大整数,
求证: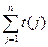
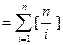 .
.
已知椭圆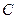 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在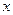 轴上,离心率为
轴上,离心率为 ,椭圆
,椭圆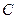 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为 .
.
(Ⅰ)求椭圆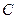 的标准方程;
的标准方程;
(Ⅱ)若过点 的直线
的直线 与椭圆
与椭圆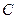 交于不同的两点
交于不同的两点 ,且
,且 ,求实数
,求实数 的取值范围.
的取值范围.
已知函数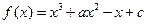 ,且
,且 .
.
(Ⅰ)求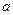 的值;
的值;
(Ⅱ)求函数 的单调区间;
的单调区间;
(Ⅲ)设函数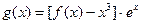 ,若函数
,若函数 在
在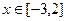 上单调递增,求实数
上单调递增,求实数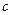 的取值范围.
的取值范围.
某高校在2011年的自主招生考试成绩
中随机抽取100名学生的笔试成绩,按成绩
分组:第1组[75,80),第2组[80,85),
第3组[85,90),第4组[90,95),第5组
[95,100]得到的频率分布直方图如图所示.
(Ⅰ)分别求第3,4,5组的频率;
(Ⅱ)若该校决定在笔试成绩高的第3,4,5组
中用分层抽样抽取6名学生进入第二轮面
试,求第3,4,5组每组各抽取多少名学生进入第二轮面试?
(Ⅲ)在(Ⅱ)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有一名学生被甲考官面试的概率.
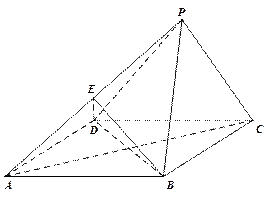
已知四棱锥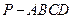 的底面是菱形.
的底面是菱形.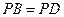 ,
,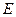 为
为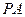 的中点.
的中点.
(Ⅰ)求证: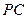 ∥平面
∥平面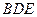 ;
;
(Ⅱ)求证:平面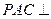 平面
平面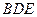 .
.