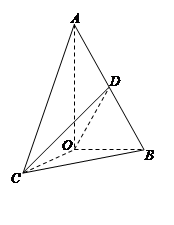某高校在2011年的自主招生考试成绩
中随机抽取100名学生的笔试成绩,按成绩
分组:第1组[75,80),第2组[80,85),
第3组[85,90),第4组[90,95),第5组
[95,100]得到的频率分布直方图如图所示.
(Ⅰ)分别求第3,4,5组的频率;
(Ⅱ)若该校决定在笔试成绩高的第3,4,5组
中用分层抽样抽取6名学生进入第二轮面
试,求第3,4,5组每组各抽取多少名学生进入第二轮面试?
(Ⅲ)在(Ⅱ)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有一名学生被甲考官面试的概率.
抛掷两颗骰子,求:
(Ⅰ)点数之和出现7点的概率;(Ⅱ)出现两个4点的概率.
 :对任意实数
:对任意实数 都有
都有 恒成立;
恒成立; :关于
:关于 的方程
的方程 有实数根;如果
有实数根;如果 与
与 中有且仅有一个为真命题,求实数
中有且仅有一个为真命题,求实数 的取值范围.
的取值范围.
已知函数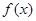 是定义在
是定义在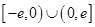 上的奇函数,当
上的奇函数,当 时,
时, 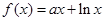 (其中e是自然界对数的底,
(其中e是自然界对数的底, )
)
(Ⅰ)设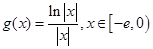 ,求证:当
,求证:当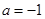 时,
时, ;
;
(Ⅱ)是否存在实数a,使得当 时,
时,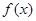 的最小值是3 ?如果存在,求出实数a的值;如果不存在,请说明理由。
的最小值是3 ?如果存在,求出实数a的值;如果不存在,请说明理由。
在直角坐标系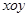 上取两个定点
上取两个定点 ,再取两个动点
,再取两个动点
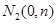 ,且
,且 .
.
(Ⅰ)求直线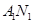 与
与 交点的轨迹
交点的轨迹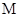 的方程;
的方程;
(Ⅱ)已知点 (
( )是轨迹
)是轨迹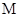 上的定点,
上的定点,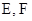 是轨迹
是轨迹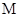 上的两个动点,如果直线
上的两个动点,如果直线 的斜率
的斜率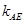 与直线
与直线 的斜率
的斜率 满足
满足 ,试探究直线
,试探究直线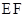 的斜率是否是定值?若是定值,求出这个定值,若不是,说明理由.
的斜率是否是定值?若是定值,求出这个定值,若不是,说明理由.
如图,已知△AOB,∠AOB= ,∠BAO=
,∠BAO= ,AB=4,D为线段AB的中点.若△AOC是△AOB绕直线AO旋转而成的.记二面角B-AO-C的大小为
,AB=4,D为线段AB的中点.若△AOC是△AOB绕直线AO旋转而成的.记二面角B-AO-C的大小为 .
.
(Ⅰ)当平面COD⊥平面AOB时,求 的值;
的值;
(Ⅱ)当 ∈[
∈[ ,
, ]时,求二面角C-OD-B的余弦值的取值范围.
]时,求二面角C-OD-B的余弦值的取值范围.