已知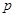 :直线
:直线 的图象不经过第二象限,
的图象不经过第二象限, :方程
:方程 表示焦点在
表示焦点在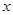 轴上的椭圆,若
轴上的椭圆,若 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围.
已知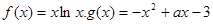
(1)求函数 在
在 上的最小值;
上的最小值;
(2)对一切 恒成立,求实数
恒成立,求实数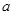 的取值范围.
的取值范围.
在△ABC中, 分别为内角A.B.C所对的边,且满足
分别为内角A.B.C所对的边,且满足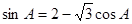
(1)求角A的大小
(2)现给出三个条件:① ②
②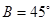 ③
③ 试从中选出两个可以确定△ABC的条件写出你的选择,并以此为依据求△ABC的面积(只需写出一个选定方案即可,选多种方案以第一种方案记分)
试从中选出两个可以确定△ABC的条件写出你的选择,并以此为依据求△ABC的面积(只需写出一个选定方案即可,选多种方案以第一种方案记分)
已知函数 .
.
(1)若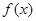 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
(2)若 是
是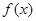 的极值点,求
的极值点,求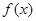 在
在 上的最小值和最大值.
上的最小值和最大值.
命题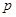 :关于
:关于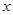 的不等式
的不等式 ,对一切
,对一切 恒成立,命题
恒成立,命题 :函数
:函数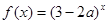 是增函数,若
是增函数,若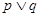 为真,
为真, 为假,求实数
为假,求实数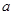 的取值范围.
的取值范围.
(本小题满分13分)已知函数
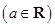 .
.
(1)若 为
为 的极值点,求实数
的极值点,求实数 的值;
的值;
(2)若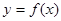 在
在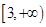 上为增函数,求实数
上为增函数,求实数 的取值范围;
的取值范围;
(3)当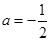 时,方程
时,方程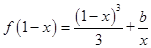 有实根,求实数
有实根,求实数 的最大值.
的最大值.