本小题满分12分)
如图,已知AB⊥平面ACD,DE//AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点。
( I )求证:AF//平面BCE;
( II)求证:平面BCE⊥平面CDE;
(III)求平面BCE与平面ACD所成锐二面角的大小。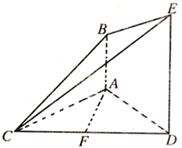
(本小题满分12分)
已知向量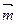 ="(sinA" ,sinB),
="(sinA" ,sinB), =(cosB,cosA),
=(cosB,cosA),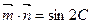 且A、B、C分别为△ABC的三边
且A、B、C分别为△ABC的三边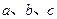 所对的角。
所对的角。
(Ⅰ)求角C的大小;
(Ⅱ)若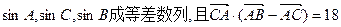 ,求c边的长。
,求c边的长。
(本小题满分12分)
已知 是等差数列,其中
是等差数列,其中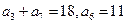 .
.
(Ⅰ)求数列 通项
通项 ;
;
(Ⅱ)若数列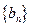 满足
满足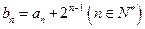 ,求数列
,求数列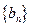 的前
的前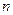 项和
项和 .
.
(本小题满分14分)
设 是椭圆
是椭圆 上的两点,点
上的两点,点 是线段
是线段 的中点,线段
的中点,线段 的垂直平分线与椭圆交于
的垂直平分线与椭圆交于 两点.
两点.
(Ⅰ)当 时,过点P(0,1)且倾斜角为
时,过点P(0,1)且倾斜角为 的直线与椭圆相交于E、F两点,求
的直线与椭圆相交于E、F两点,求 长;
长;
(Ⅱ)确定 的取值范围,并求直线CD的方程.
的取值范围,并求直线CD的方程.
(本小题满分12分)
已知抛物线C的顶点在原点,焦点在x轴上,且抛物线上有一点 (4,
(4, )到焦点的距离为5.
)到焦点的距离为5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)若抛物线C与直线 相交于不同的两点A、B,求证:
相交于不同的两点A、B,求证:
 .
.