观察下列等式,
-1× =-1+
=-1+ ,-
,- ×
× =-
=- +
+ ,-
,- ×
× =-
=- +
+ ,……
,……
(1)你发现的规律是 (用含n的式子表示,n为正整数)
(2)运用以上规律计算:
(-1× )+(-
)+(- ×
× )+(-
)+(- ×
× )+…+(
)+…+( )
)
在平面直角坐标系xOy中,横、纵坐标都为整数的点称为整点.已知一组正方形的四个顶点恰好落在两坐标轴上,请你观察每个正方形四条边上的整点的个数的变化规律.
回答下列问题:
(1)经过x轴上点(5,0)的正方形的四条边上的整点个数是;
(2)经过x轴上点(n,0)(n为正整数)的正方形的四条边上的整点个数记为m,则m与n之间的函数关系是.
在△ABC中,AD是△ABC的角平分线.
(1)如图1,过C作CE∥AD交BA延长线于点E,若F为CE的中点,连结AF,求证:AF⊥AD;
(2)如图2,M为BC的中点,过M作MN∥AD交AC于点N,若AB=4, AC=7,
求NC的长.
已知:一次函数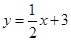 的图象与正比例函数
的图象与正比例函数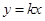 的图象相交于点
的图象相交于点
A(a,1).
(1)求a的值及正比例函数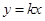 的解析式;
的解析式;
(2)点P在坐标轴上(不与点O重合),若PA=OA,直接写出P点的坐标;
(3)直线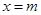 与一次函数的图象交于点B,与正比例函数图象交于点C,若△ABC的面积记为S,求S关于m的函数关系式(写出自变量的取值范围).
与一次函数的图象交于点B,与正比例函数图象交于点C,若△ABC的面积记为S,求S关于m的函数关系式(写出自变量的取值范围).
阅读下列材料:
木工张师傅在加工制作家具的时候,用下面的方法在木板上画直角:
如图1,他首先在需要加工的位置画一条线段AB,接着分别以点A、点B为圆心,以大于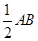 的适当长为半径画弧,两弧相交于点C,再以C为圆心,以同样长为半径画弧交AC的延长线于点D(点D需落在木板上),连接DB.则∠ABD就是直角.
的适当长为半径画弧,两弧相交于点C,再以C为圆心,以同样长为半径画弧交AC的延长线于点D(点D需落在木板上),连接DB.则∠ABD就是直角.
木工张师傅把上面的这种作直角的方法叫做“三弧法.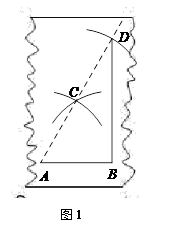
解决下列问题:
(1)利用图1就∠ABD是直角作出合理解释 (要求:先写出已知、求证,再进行证明);
(2)图2表示的一块残缺的圆形木板,请你用“三弧法”,在木板上画出一个以EF为一条直角边的直角三角形EFG(要求:尺规作图,不写作法,保留作图痕迹).
如图,直线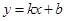 经过点A(0,5),B(1,4).
经过点A(0,5),B(1,4).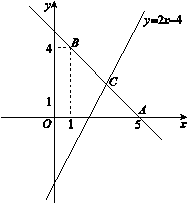
(1)求直线AB的解析式;
(2)若直线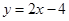 与直线AB相交于点C,求点C的坐标;
与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x-4≥kx+b的解集.