某商店购进600个旅游纪念品,进价为每个6元,第一周以每个10元的价格售出200个,第二周若按每个10元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价),单价降低x元销售销售一周后,商店对剩余旅游纪念品清仓处理,以每个4元的价格全部售出,如果这批旅游纪念品共获利1050元,问第二周每个旅游纪念品的销售价格为多少元?
如图,已知射线DM与直线BC交于点A,AB∥DE.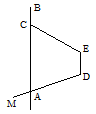
(1)若当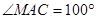 ,
,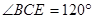 时,问把EC绕点E再旋转多大角度时,可判定MD∥EC,请你设计出两种方案,并画出草图(旋转后若EC与AB相交,则交点用
时,问把EC绕点E再旋转多大角度时,可判定MD∥EC,请你设计出两种方案,并画出草图(旋转后若EC与AB相交,则交点用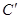 表示).
表示).
(2)若将EC绕点E逆时针旋转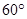 时,点C与点A恰好重合,请画出草图,并在图中找出同位角、内错角各两对(先用数字标出角,再回答).
时,点C与点A恰好重合,请画出草图,并在图中找出同位角、内错角各两对(先用数字标出角,再回答).
如图,四边形ABCD中,∠A ="∠C=" 90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由。
请你在下图中建立适当的直角坐标系,并写出各地点的坐标。。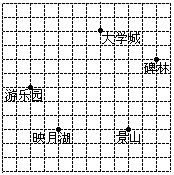
如图,△ABC中,点D在BC的延长线上,过D作DE⊥AB于E,交AC于F。已知∠A=30°,∠FCD=80°,求∠D的度数。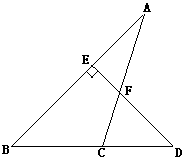
在图所示的平面直角坐标系中表示下面各点:。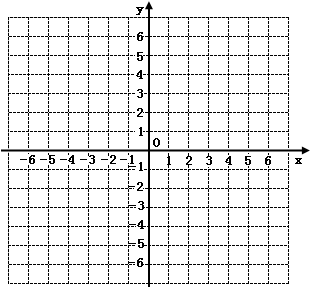
A(0,3),B(1,-3),C(3,-5),D(-3,-5),E(3,5),F(5,7)。
(1)A点到原点O的距离是__ __个单位长。
(2)将点C向左平移6个单位,它会与点重合。
(3)连接CE,则直线CE与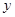 轴是什么位置关系?
轴是什么位置关系?
(4)点F到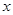 、
、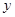 轴的距离分别是多少?
轴的距离分别是多少?