如图，内径均匀的弯曲玻璃管ABCDE两端开口，AB、CD段竖直，BC、DE段水平，AB=100cm，BC=40cm，CD=50cm，DE=60cm。在水平段DE内有一长10cm的水银柱，其左端距D点10cm。在环境温度为300 K时，保持BC段水平，将玻璃管A端缓慢竖直向下插入大水银槽中，使A端在水银面下10 cm。已知大气压为75 cmHg且保持不变。
（1）若环境温度缓慢升高，求温度升高到多少K时，水银柱刚好全部溢出；
（2）若环境温度缓慢降低，求温度降低到多少K时，水银柱刚好全部进入CD段。
核聚变能是一种具有经济性能优越、安全可靠、无环境污染等优势的新能源。近年来，受控核聚变的科学可行性已得到验证，目前正在突破关键技术，最终将建成商用核聚变电站。一种常见的核聚变反应是由氢的同位素氘（又叫重氢）和氚（又叫超重氢）聚合成氦，并释放一个中子。若已知氘原子的质量为2.0141u，氚原子的质量为3.0160u，氦原子的质量为4.0026u，中子的质量为1.0087u，1u＝1.66×10-27kg。
（1）写出氘和氚聚合的反应方程。
（2）试计算这个核反应释放出来的能量。
（3）若建一座功率为3.0×105kw的核聚变电站，假设聚变所产生的能量有一半变成了电能，每年要消耗多少氘的质量？（一年按3.2×107s计算，光速c＝3.00×108m/s，结果取二位有效数字）
如图所示为伦琴射线管的示意图,K为阴极,A为对阴极,假设由K极发射的电子初速度为零,当AK之间所加直流电压U=30kV时,电子被加速打在对阴极A上,使之发射出伦琴射线,设电子的动能全部转化为伦琴射线的能量.已知电子电量e=1.6×10-19c,质量m=0.91×10-30kg,普朗克常数h=6.63×10-34J·s,问：
(1)电子到达对阴极的速度多大(取一位有效数字)
(2)由对阴极发出的伦琴射线的最短波长多大?
(3)若AK间的电流为10mA,那么每秒从对阴极最多能辐射多少个伦琴射线光子?
半径为R的半圆柱形玻璃砖，横截面如图所示。O为圆心。已知玻璃的折射率为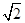
。当光由玻璃射向空气时，发生全反射的临界角为45°，一束与MN平面成450的平行光束射到玻璃砖的半圆柱面上，经玻璃折射后，有部分光能从MN平面上射出。求能从MN平面射出的光束的宽度为多少？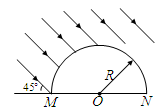
一个电源的路端电压U随外电路电阻R的变化规律如图(甲)所示，图中U＝12 V的直线为图线的渐近线．现将该电源和一个变阻器R0接成如图(乙)所示电路，已知电源允许通过的最大电流为2 A，变阻器的最大阻值为R0＝22 Ω.求：
(1)电源电动势E和内电阻r；
(2)空载时A、B两端输出的电压范围．
(3)A、B两端所能接负载的电阻的最小值．
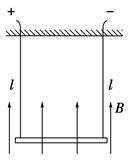
如图所示，质量为0.05 kg、长l＝0.1 m的铜棒，用长度也为l的两根轻软导线水平悬吊在竖直向上的匀强磁场中，磁感应强度为B＝0.5 T．不通电时，轻线在竖直方向，通入恒定电流后，棒向外偏转的最大角度θ＝37°，求此棒中恒定电流多大？(不考虑棒摆动过程中产生的感应电流，g取10 N/kg)