(本小题满分12分)季节性服装当季节即将来临时,价格呈上升趋势,设某服装开始时定价为10元,并且每周(7天)涨价2元,5周后开始保持20元的价格平稳销售;10周后当季节即将过去时,平均每周削价2元,直到16周末,该服装已不再销售.
(1)试建立价格P与周次t之间的函数关系式;
(2)若此服装每件进价Q与周次t之间的关系为 ,
,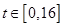 ,
,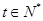 ,试问该服装第几周每件销售利润最大,最大值是多少?
,试问该服装第几周每件销售利润最大,最大值是多少?
(注:每件销售利润=售价-进价)
(本小题满分12分)在 中,角
中,角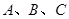 所对的边为
所对的边为 ,且满足
,且满足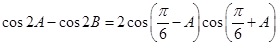
(1)求角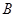 的值;
的值;
(2)若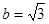 且
且 ,求
,求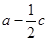 的取值范围.
的取值范围.
(本小题满分10分)已知圆 :
: 关于直线
关于直线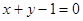 对称,圆心
对称,圆心 在第四象限,半径为
在第四象限,半径为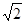 .
.
(Ⅰ)求圆 的方程;
的方程;
(Ⅱ)是否存在直线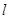 与圆
与圆 相切,且在
相切,且在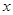 轴上的截距是y轴上的截距的
轴上的截距是y轴上的截距的 倍?若存在,求直线
倍?若存在,求直线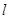 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(本小题满分10分)
如图,平面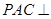 平面
平面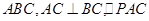 为等边三角形,
为等边三角形, 分别是线段
分别是线段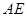 ,
, 上的动点,且满足:
上的动点,且满足: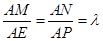
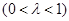 .
.
(Ⅰ)求证: ∥平面
∥平面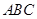 ;
;
(Ⅱ)当 时,求平面ABC与平面MNC所成的锐二面角的大小.
时,求平面ABC与平面MNC所成的锐二面角的大小.
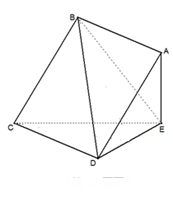
(本小题满分10分)如图,在四棱锥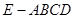 中,底面
中,底面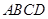 为正方形,
为正方形, 平面
平面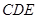 ,已知
,已知 .
.
(Ⅰ)求证:平面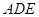
 平面
平面 ;
;
(Ⅱ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
如图,直线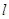 过点
过点 ,夹在两已知直线
,夹在两已知直线 和
和 之间的线段
之间的线段 恰被点
恰被点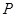 平分.
平分.
(Ⅰ)求直线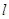 的方程;
的方程;
(Ⅱ)设点 ,且
,且 ,求:
,求: 的面积.
的面积.