如图是一个直三棱柱被削去一部分后的几何体的直观图与三视图中的侧视图、俯视图.在直观图中,M是BD的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(1)求证:ME∥平面ABC;
(2)试问在棱DC上是否存在点N,使NM⊥平面BDE? 若存在,确定点N的位置;若不存在,请说明理由.
已知正四棱柱 的底面边长为2,
的底面边长为2, .
.
(1)求该四棱柱的侧面积与体积;
(2)若 为线段
为线段 的中点,求
的中点,求 与平面
与平面 所成角的大小.
所成角的大小.
已知函数 ,
, (其中
(其中 ,
, ),且函数
),且函数 的图象在点
的图象在点 处的切线与函数
处的切线与函数 的图象在点
的图象在点 处的切线重合.
处的切线重合.
(Ⅰ)求实数a,b的值;
(Ⅱ)若 ,满足
,满足 ,求实数m的取值范围;
,求实数m的取值范围;
如图,F1,F2是离心率为 的椭圆
的椭圆
C: (a>b>0)的左、右焦点,直线
(a>b>0)的左、右焦点,直线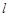 :x=-
:x=- 将线段F1F2分成两段,其长度之比为1 :3.设A,B是C上的两个动点,线段AB的中点M在直线l上,线段AB的中垂线与C交于P,Q两点.
将线段F1F2分成两段,其长度之比为1 :3.设A,B是C上的两个动点,线段AB的中点M在直线l上,线段AB的中垂线与C交于P,Q两点.
(Ⅰ) 求椭圆C的方程;
(Ⅱ) 是否存在点M,使以PQ为直径的圆经过点F2,若存在,求出M点坐标,若不存在,请说明理由.
已知 ,数列
,数列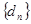 满足
满足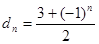 ,数列
,数列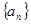 满足
满足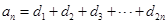 ;又知数列
;又知数列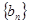 中,
中,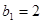 ,且对任意正整数
,且对任意正整数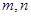 ,
,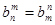 .
.
(Ⅰ)求数列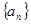 和数列
和数列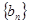 的通项公式;
的通项公式;
(Ⅱ)将数列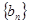 中的第
中的第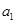 项,第
项,第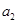 项,第
项,第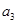 项,……,第
项,……,第 项,……删去后,剩余的项按从小到大的顺序排成新数列
项,……删去后,剩余的项按从小到大的顺序排成新数列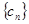 ,求数列
,求数列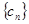 的前
的前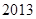 项和.
项和.
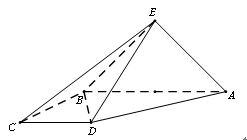
(本小题满分12分)如图,直角梯形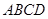 与等腰直角三角形
与等腰直角三角形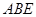 所在的平面互相垂直.
所在的平面互相垂直.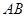 ∥
∥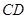 ,
,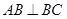 ,
,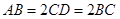 ,
,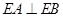 .
.
(1)求直线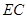 与平面
与平面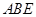 所成角的正弦值;
所成角的正弦值;
(2)线段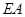 上是否存在点
上是否存在点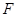 ,使
,使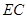 // 平面
// 平面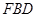 ?若存在,求出
?若存在,求出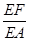 ;若不存在,说明理由.1
;若不存在,说明理由.1