(本小题满分12分)如图,在三棱锥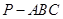 中,
中,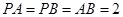 ,
,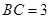 ,
,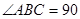 °,平面
°,平面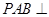 平面
平面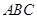 ,
,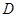 ,
, 分别为
分别为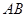 ,
, 中点.
中点.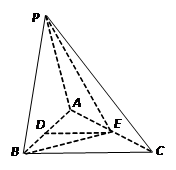
(1)求证: ∥平面
∥平面 ;
;
(2)求证: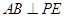 ;
;
(3)求三棱锥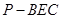 的体积.
的体积.
22.已知抛物线C的顶点在原点,焦点在y轴正半轴上,点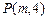 到其准线的距离等于5.
到其准线的距离等于5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)如图,过抛物线C的焦点的直线从左到右依次与抛物线C及圆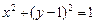 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明 为定值;
为定值;
|
(Ⅲ)过A、B分别作抛物C的切线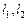 且
且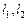 交于点M,求
交于点M,求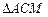 与
与 面积之和的最小值.
面积之和的最小值.
已知函数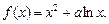
(Ⅰ)当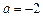 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅱ)若 在
在 是单调函数,求实数
是单调函数,求实数 的取值范围.
的取值范围.
如图,在四棱锥E-ABCD中,底面ABCD为正方形, AE⊥平面CDE,已知AE=3,DE=4.
(Ⅰ)若F为DE的中点,求证:BE//平面ACF;
(Ⅱ)求直线BE与平面ABCD所成角的正弦值.
设向量 ,函数
,函数 (其中
(其中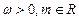 ).且
).且 的图像在y轴右侧的第一个最高点的横坐标是
的图像在y轴右侧的第一个最高点的横坐标是
(Ⅰ)求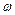 的值和
的值和 单调增区间;
单调增区间;
(Ⅱ)如果 在区间
在区间 上的最小值为
上的最小值为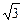 ,求m的值
,求m的值
已知函数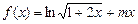 .
.
(Ⅰ)若 为定义域上的单调函数,求实数m的取值范围;
为定义域上的单调函数,求实数m的取值范围;
(Ⅱ)当 时,求函数
时,求函数 的最大值;
的最大值;
(Ⅲ)当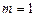 ,且
,且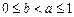 时,证明:
时,证明: .
.