(本小题满分12分)已知圆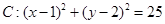 ,直线
,直线 ,
,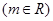 。
。
(1)证明:不论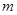 取什么实数,直线
取什么实数,直线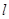 与圆恒交于两点;
与圆恒交于两点;
(2)求直线被圆 截得的弦长最小时
截得的弦长最小时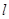 的方程.
的方程.
椭圆 的方程为
的方程为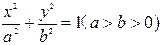 ,斜率为1的直线
,斜率为1的直线 与椭圆
与椭圆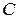 交于
交于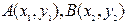 两点.
两点.
(Ⅰ)若椭圆的离心率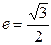 ,直线
,直线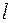 过点
过点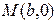 ,且
,且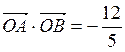 ,求椭圆
,求椭圆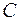 的方程;
的方程;
(Ⅱ)直线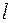 过椭圆的右焦点F,设向量
过椭圆的右焦点F,设向量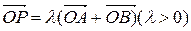 ,若点
,若点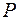 在椭圆
在椭圆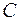 上,求
上,求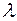 的取值范围.
的取值范围.
如图,直四棱柱 中,底面
中,底面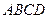 是
是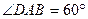 的菱形,
的菱形, ,
,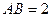 ,点
,点 在棱
在棱 上,点
上,点 是棱
是棱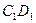 的中点.
的中点.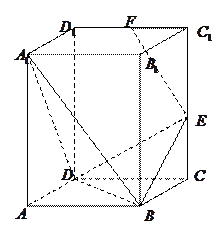
(1)若 是
是 的中点,求证:
的中点,求证: ;
;
(2)求出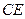 的长度,使得
的长度,使得 为直二面角.
为直二面角.
某射击小组有甲、乙两名射手,甲的命中率为
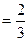 ,乙的命中率为
,乙的命中率为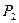 ,在射击比武活动中每人射击两发子弹则完成一次检测,在一次检测中,若两人命中次数相等且都不少于一发,则称该射击小组为“先进和谐组”.
,在射击比武活动中每人射击两发子弹则完成一次检测,在一次检测中,若两人命中次数相等且都不少于一发,则称该射击小组为“先进和谐组”.
(Ⅰ)若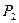
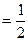 ,求该小组在一次检测中荣获“先进和谐组”的概率;
,求该小组在一次检测中荣获“先进和谐组”的概率;
(Ⅱ)计划在2011年每月进行1次检测,设这12次检测中该小组获得“先进和谐组”的次数为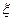 , 如果
, 如果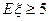 ,求
,求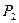 的取值范围;
的取值范围;
已知函数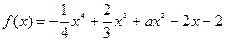 在区间
在区间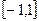 上单调递减,在区间
上单调递减,在区间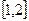 上单调递增.
上单调递增.
(Ⅰ)求实数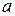 的值;
的值;
(Ⅱ)若关于 的方程
的方程 有三个不同实数解,求实数
有三个不同实数解,求实数 的取值范围;
的取值范围;
(Ⅲ)若函数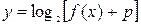 的图象与坐标轴无交点,求实数
的图象与坐标轴无交点,求实数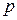 的取值范围.
的取值范围.
设定义在R上的函数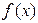 满足:①
满足:① 对任意的实数
对任意的实数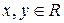 ,有
,有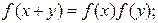 ②当
②当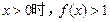 .
.
数列 满足
满足 .
.
(1)求证: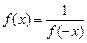 ,并判断函数
,并判断函数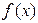 的单调性;
的单调性;
(2)令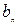 是最接近
是最接近 的正整数,即
的正整数,即 ,
,
设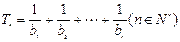 ,求
,求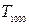 ;
;