(本小题满分12分)如图,四棱锥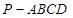 的底面是正方形,
的底面是正方形,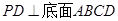 ,点
,点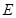 在棱
在棱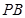 上.
上.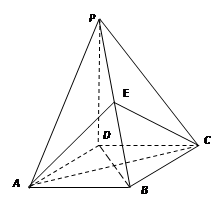
(1)求证:平面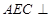 平面
平面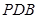 ;
;
(2)当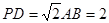 ,且
,且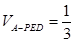 时,确定点
时,确定点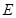 的位置,即求出
的位置,即求出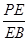 的值.
的值.
(本小题满分12分)设二次函数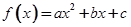 在区间
在区间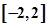 上的最大值、最小值分别是M、m,集合
上的最大值、最小值分别是M、m,集合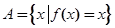 .
.
(Ⅰ)若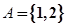 ,且
,且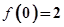 ,求M和m的值;
,求M和m的值;
(Ⅱ)若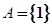 ,且
,且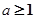 ,记
,记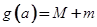 ,求
,求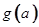 的最小值.
的最小值.
(本小题满分12分)已知在直角坐标系xoy中,曲线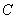 的参数方程为
的参数方程为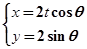
(t为非零常数,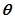 为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以
为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以 轴正半轴为极轴)中,直线
轴正半轴为极轴)中,直线 的方程为
的方程为 .
.
(Ⅰ)求曲线C的普通方程并说明曲线的形状;
(Ⅱ)是否存在实数 ,使得直线
,使得直线 与曲线C有两个不同的公共点
与曲线C有两个不同的公共点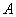 、
、 ,且
,且
(其中o为坐标原点)?若存在,请求出;否则,请说明理由
(本小题满分12分)已知c>0,设命题p:函数y=cx为减函数.命题q:当x∈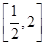 时,函数f(x)=x+>恒成立.如果p或q为真命题,p且q为假命题.求c的取值范围.
时,函数f(x)=x+>恒成立.如果p或q为真命题,p且q为假命题.求c的取值范围.
设函数
(Ⅰ)求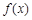 的单调区间;
的单调区间;
(Ⅱ)证明:当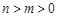 时,
时, ;
;
(Ⅲ)证明:当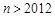 ,且
,且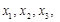 …,
…,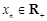 ,
,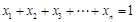 时,
时,
(1)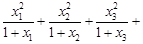 …
…
(2) 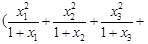 …
… .
.
已知椭圆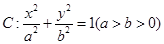 的离心率为
的离心率为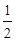 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线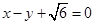 相切,直线
相切,直线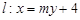 与椭圆C相交于A、B两点.
与椭圆C相交于A、B两点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)求 的取值范围;
的取值范围;
(Ⅲ)若B点关于x轴的对称点是E,证明:直线AE与x轴相交于定点.