已知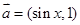 ,
, ,若
,若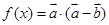 ,求:
,求:
(1)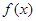 的最小正周期及对称轴方程.
的最小正周期及对称轴方程.
(2)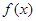 的单调递增区间.
的单调递增区间.
(3)当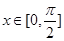 时,函数
时,函数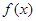 的值域.
的值域.
(13分)如图(3):四面体D—ABC中,DB⊥面ABC, ∠DAB="30°,∠BAC=45°," ∠ACB=90°.BC=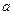 .
.
(1)点A与面BCD的距离; (2)AB与CD成的角的余弦值.
(13分)已知点A(2,8),B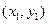 ,C
,C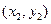 都在抛物线
都在抛物线 上,△ABC的重心与此抛物线E的焦点F重合. (1)写出抛物线E的方程及焦点坐标; (2)求线段BC的中点M的坐标及BC边所在的直线方程.
上,△ABC的重心与此抛物线E的焦点F重合. (1)写出抛物线E的方程及焦点坐标; (2)求线段BC的中点M的坐标及BC边所在的直线方程.
(13分)如图(2):PA⊥面ABCD,CD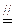 2AB,
2AB,
∠DAB=90°,E为PC的中点.
(1)证明:BE//面PAD;
(2)若PA=AD,证明:BE⊥面PDC.
已知抛物线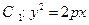 的准线方程为
的准线方程为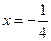 ,与直线
,与直线
在第一象限相交于点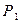 ,过
,过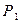 作
作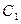 的切线
的切线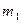 ,过
,过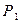 作
作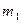 的垂线
的垂线 交x轴正
交x轴正
半轴于点 ,过
,过 作
作 的平行线
的平行线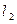 交抛物线于第一象限内的点
交抛物线于第一象限内的点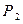 ,过
,过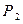 作
作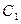 的切线
的切线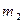 ,过
,过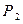 作
作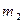 的垂线
的垂线 交x轴正半轴于点
交x轴正半轴于点 ,依此类推,在x
,依此类推,在x
轴上形成一点列 ,
, ,
,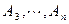 (
( )设
)设 的坐标为(
的坐标为( )
)
(Ⅰ)求抛物线的方程;(Ⅱ)试探求 关于
关于 的递推关系;
的递推关系;
已知函数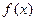 =
= 的图象与直线
的图象与直线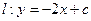 相切,切点的横坐标为1。(Ⅰ)求函数
相切,切点的横坐标为1。(Ⅰ)求函数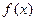 的表达式和直线
的表达式和直线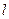 的方程;(Ⅱ)求函数
的方程;(Ⅱ)求函数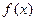 的单调区间;(Ⅲ)若不等式
的单调区间;(Ⅲ)若不等式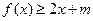 对
对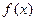 定义域内的任意x恒成立,求实数m的取值范围。
定义域内的任意x恒成立,求实数m的取值范围。