(本小题满分13分)已知数列 满足:
满足: ,数列
,数列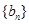 满足:
满足: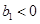 ,
, ,数列
,数列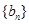 的前
的前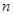 项和为
项和为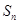 .
.
(Ⅰ)求证:数列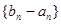 为等比数列;
为等比数列;
(Ⅱ)求证:数列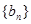 为递增数列;
为递增数列;
(Ⅲ)若当且仅当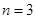 时,
时,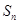 取得最小值,求
取得最小值,求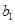 的取值范围.
的取值范围.
在△ABC中,a, b, c分别为内角A, B, C的对边,且满足2asinA=(2b+c)sinB+(2c+b)sinC
(Ⅰ)求A的大小;(Ⅱ)求 的最大值.
的最大值.
)已知数列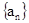 是等差数列,其前n项和为
是等差数列,其前n项和为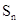 ,
, ,
,
(I)求数列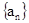 的通项公式;
的通项公式;
(II)设p、q是正整数,且p≠q. 证明: .
.
)已知二次函数f(x)=
(1)若f(0)>0,求实数p的取值范围
(2)在区间[-1,1]内至少存在一个实数c,使f(c)>0,求实数p的取值范围。
直线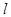 经过点P(-5,-4),且与两坐标轴围成的三角形面积为5,求直线
经过点P(-5,-4),且与两坐标轴围成的三角形面积为5,求直线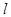 的方程。
的方程。
已知函数f(x)= ,g(x)=2|x|+a.
,g(x)=2|x|+a.
(1)当a=0时,解不等式f(x)≥g(x);
(2)若存在x∈ R,使得f(x)≥g(x)成立,求实数a的取值范围.