设椭圆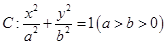 的左、右焦点分别为
的左、右焦点分别为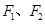 ,上顶点为
,上顶点为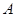 ,在
,在 轴负半轴上有一点
轴负半轴上有一点 ,满足
,满足 ,且
,且 .
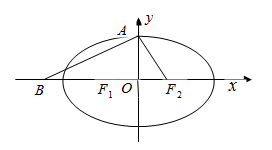
.
(1)求椭圆 的离心率;
的离心率;
(2)若过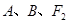 三点的圆与直线
三点的圆与直线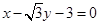 相切,求椭圆
相切,求椭圆 的方程;
的方程;
(3)在(2)的条件下,过右焦点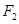 作斜率为
作斜率为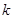 的直线
的直线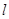 与椭圆
与椭圆 交于
交于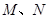 两点,线段
两点,线段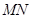 的中垂线与
的中垂线与 轴相交于
轴相交于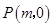 ,求实数
,求实数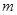 的取值范围.
的取值范围.
(本小题满分14分)
设函数 ,函数g(x)=
,函数g(x)= 分别在x=m和x=n处取得极值,且
分别在x=m和x=n处取得极值,且
m<n
(1)求 的值
的值
(2)求证:f(x)在区间[m,n]上是增函数
(3)设f(x)在区间[m,n]上的最大值和最小值分别为M和N,试问当实数a为何值时,M-N取得最小值?并求出这个最小值
(本小题满分12分)
设数列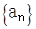 的前n项和为
的前n项和为 且方程
且方程 有一根为
有一根为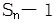 ,n=1,2,3…,试求
,n=1,2,3…,试求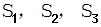 的值,猜想
的值,猜想 的表达式,并用数学归纳法加以证明
的表达式,并用数学归纳法加以证明
(本小题满分12分)
某商场从生产厂家以每件20元的价格购进一批商品,该商品的销售量Q(单位:
件)与零售价p(单位:元)有如下关系为
Q=8300-170p- ,求该商品零售价定为多少元时,毛利润L最大,并求出最大毛利润(毛利润=销售收入-进货支出)
,求该商品零售价定为多少元时,毛利润L最大,并求出最大毛利润(毛利润=销售收入-进货支出)
(本小题满分12分)
若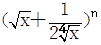 的展开式中前三项系数成等差数列,求:
的展开式中前三项系数成等差数列,求:
(1)展开式中所有的有理项
(2)展开式中系数最大项
(本小题满分12分)
已知曲线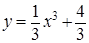
(1)求曲线在点P(2,4)处的切线方程
(2)求曲线在点P(2,4)的切线方程
(3)求斜率为4的曲线的切线方程