(本小题满分12分)某市为了解全市居民日常用水量的分布情况,现采用抽样调查的方式,获得了n位居民某年的月均用水量(单位:t),样本统计结果如下图表:
| 分组 |
频数 |
频率 |
| [0,1) |
25 |
y |
| [1,2) |
|
0.19 |
| [2,3) |
50 |
x |
| [3,4) |
|
0.23 |
| [4,5) |
|
0.18 |
| [5,6] |
5 |
|

(Ⅰ)分别求出x,n,y的值;
(Ⅱ)若从样本中月均用水量在[5,6]内的5位居民a,b,c,d,e中任选2人作进一步的调查研究,求居民a被选中的概率.
甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次.记录如下:
甲:82 81 79 78 95 88 93 84
乙:92 95 80 75 83 80 90 85
(1)画出甲、乙两位学生成绩的茎叶图,指出学生乙成绩的中位数.并说明它在乙组数据中的含义;
(2)现要从中选派一人参加数学竞赛,从平均状况和方差的角度考虑,你认为派哪位学生参加合适?请说明理由;
(3)若将频率视为概率,对学生甲在今后的三次数学竞赛成绩进行预测,记这三次成绩中高于80分的次数为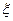 ,求
,求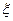 的分布列及数学期望.
的分布列及数学期望.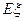
如图的多面体是底面为平行四边形的直四棱柱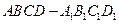 ,经平面
,经平面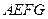 所截后得到的图形.其中
所截后得到的图形.其中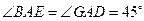 ,
,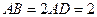 ,
,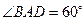 .
.
(1)求证: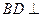 平面
平面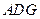 ;
;
(2)求平面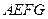 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.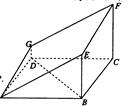
(本题满分12)
已知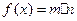 ,其中
,其中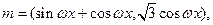
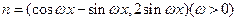 .若
.若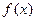 图象中相邻的对称轴间的距离不小于
图象中相邻的对称轴间的距离不小于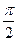 .
.
(1)求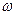 的取值范围
的取值范围
(2)在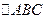 中,
中,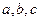 分别为角
分别为角 的对边.且
的对边.且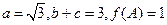 ,当
,当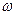 最大时.求
最大时.求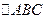 面积.
面积.
(4-5不等式选讲)(本小题10分)
设函数 .
.
⑴求不等式 的解集;
的解集;
⑵求函数 的最小值.
的最小值.
(4-4极坐标与参数方程)(本小题10分)
已知直线 的参数方程为
的参数方程为 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 (θ为参数).
(θ为参数).
⑴将曲线C的参数方程化为普通方程;
⑵若直线l与曲线C交于A、B两点,求线段AB的长.