化简 .
.
已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.
(1)求此抛物线的解析式;
(2)连接AC、BC,若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(3)在(2)的基础上试说明S是否存在最大值,若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由。
已知:如图,BD为⊙O的直径,AB=AC,AD交BC于E,AE=2,ED=4.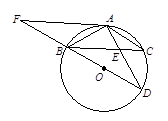
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使BF=OB,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
国家发改委公布的《商品房销售明码标价规定》,从2011年5月1日起商品房销售实行一套一标价.商品房销售价格明码标价后,可以自行降价、打折销售,但涨价必须重新申报.A市某楼盘准备以每平方米5000元的均价对外销售,由于新政策的出台,购房者持币观望.为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米4 050元的均价开盘销售.
(1)求平均每次下调的百分率;
(2)某人准备以开盘均价购买一套100平方米的房子,开发商还给予以下两种优惠方案供选择:①打9.8折销售;②不打折,送两年物业管理费,物业管理费是每平方米每月1.5元,请问哪种方案更优惠?
2013年4月20日08时02分,四川省雅安市芦山县发生7.0级地震。某地震救援队探测出某建筑物废墟下方点 C 处有生命迹象,已知废墟一侧地面上两探测点A、B 相距 3 米,探测线与地面的夹角分别是30°和 60°(如图),试确定生命所在点 C 的深度.(结果精确到0.1米,参考数据: ).
).
小张和小罗玩一种转盘游戏,如图是两个完全相同的转盘,转盘一被分成面积相等的三个扇形,用数字“1”、“2”、“3”表示,转盘二被分成面积相等的四个扇形,用数字“1”、“2”、“3”、“4”表示,固定指针,同时转动两个转盘,任其自由停止,若两指针所指数字之积为偶数,则小张获胜;若两指针所指数字之积为奇数,则小罗获胜;若其中一个指针指向扇形的分界线,则都重转一次.你认为游戏是否公平?请说明理由.若不公平,请你修改游戏规则,使游戏公平.