如图,在一次数学课外实践活动中,要求测教学楼的高度AB、小刚在D处用高1.5m的测角仪CD,测得教学楼顶端A的仰角为30°,然后向教学楼前进40m到达E,又测得教学楼顶端A的仰角为60°.求这幢教学楼的高度AB.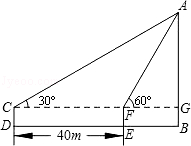
为实施“农村留守儿童关爱计划”,某校对全校各班留守儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅不完整的统计图: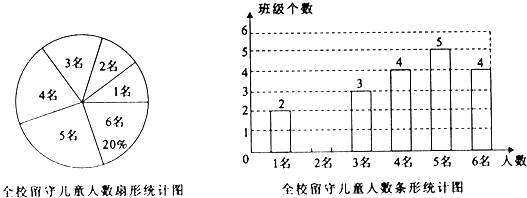
(1)求该校平均每班有多少名留守儿童?并将该条形统计图补充完整;
(2)某爱心人士决定从只有2名留守儿童的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名留守儿童来自同一个班级的概率.
在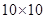 的网格纸上建立平面直角坐标系如图所示,在
的网格纸上建立平面直角坐标系如图所示,在 中,
中,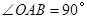 ,且点
,且点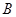 的坐标为
的坐标为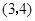 .
.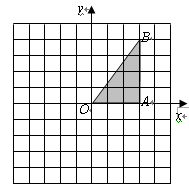
(1)画出
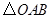 向左平移3个单位后的
向左平移3个单位后的 ,写出点
,写出点 的坐标;
的坐标;(2)画出
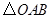 绕点
绕点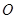 顺时针旋转
顺时针旋转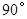 后的
后的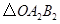 ,并求点
,并求点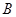 旋转到点
旋转到点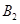 时,点
时,点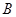 经过的路线长(结果保留
经过的路线长(结果保留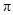 )
)
解方程: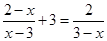
(1)计算:

(2)化简:
 .
.
如图,P为正方形ABCD的对称中心,正方形ABCD的边长为 ,
, ,直线OP交AB于N,DC于M,点H从原点O出发沿x轴的正半轴方向以1个单位每秒速度运动,同时,点R从O出发沿OM方向以
,直线OP交AB于N,DC于M,点H从原点O出发沿x轴的正半轴方向以1个单位每秒速度运动,同时,点R从O出发沿OM方向以 个单位每秒速度运动,运动时间为t,求:
个单位每秒速度运动,运动时间为t,求:
(1)直接写出A、D、P的坐标;
(2)求△HCR面积S与t的函数关系式;
(3)当t为何值时,△ANO与△DMR相似?
(4)求以A、B、C、R为顶点的四边形是梯形时t的值.