解方程: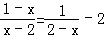 .
.
已知关于x的方程 .
.
(1)若这个方程有实数根,求k的取值范围;
(2)若这个方程有一个根为1,求k的值;
(3)若以方程 的两个根为横坐标、纵坐标的点恰在反比例函数
的两个根为横坐标、纵坐标的点恰在反比例函数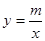 的图象上,求满足条件的m的最小值.
的图象上,求满足条件的m的最小值.
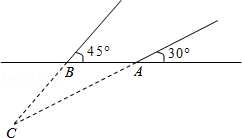
2013年3月,某煤矿发生瓦斯爆炸,该地救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A、B两个探测点探测到C处有生命迹象.已知A、B两点相距4米,探测线与地面的夹角分别是30°和45°,试确定生命所在点C的深度.(精确到0.1米,参考数据: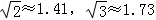 )
)
如图,四边形OABC是矩形,点A、C的坐标分别为(3,0)、(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线 交折线OAB于点E.
交折线OAB于点E.
(1)记 的面积为S,求S与b的函数关系式;
的面积为S,求S与b的函数关系式;
(2)当点E在线段OA上时,若矩形OABC关于直线DE的对称图形为四边形 ,DE=
,DE= ,试探究四边形
,试探究四边形 与矩形OABC的重叠部分的面积是否发生变化,若不变,求出该重叠部分的面积;若改变,请说明理由。
与矩形OABC的重叠部分的面积是否发生变化,若不变,求出该重叠部分的面积;若改变,请说明理由。
A、B两码头相距150千米,甲客船顺流由A航行到B,乙客船逆流由B到A,若甲、乙两客船在静水中的速度相同,同时出发,它们航行的路程y(千米)与航行时间x(时)的关系如图所示.
(1)求客船在静水中的速度及水流速度;
(2)一艘货轮由A码头顺流航行到B码头,货轮比客船早2小时出发,货轮在静水中的速度为10千米/时,在此坐标系中画出货轮航程y(千米)与时间x(时)的关系图象,并求货轮与客船乙相遇时距A码头的路程。
某景点的门票价格规定如下表
| 购票人数 |
1—50人 |
51—100人 |
100人以上 |
| 每人门票价 |
12元 |
10元 |
8元 |
某校八年(一)、(二)两班共100多人去游览该景点,其中(一)班不足50人,(二)班多于50人,如果两班都以班为单位分别购票,则一共付款1126元.如果以团体购票,则需要付费824元,问:
(1)两班各有多少名学生?
(2)如果你是学校负责人,你将如何购票?你的购票方法可节省多少钱?