(本小题满分12分)(理科做)如图,四棱锥 中,平面
中,平面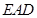
 平面
平面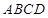 ,
,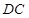 //
//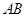 ,
, ,
, ,且
,且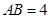 ,
,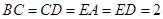 .
.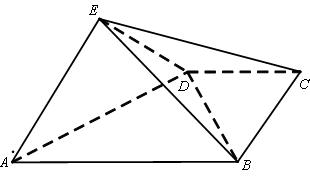
(1)求证: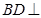 平面
平面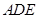 ;
;
(2)求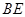 和平面
和平面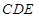 所成角的正弦值;
所成角的正弦值;
(3)在线段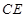 上是否存在一点
上是否存在一点 使得平面
使得平面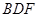
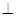 平面
平面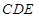 ,请说明理由.
,请说明理由.
(文科做)已知函数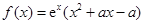 ,其中
,其中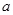 是常数.
是常数.
(1)当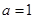 时,求曲线
时,求曲线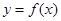 在点
在点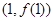 处的切线方程;
处的切线方程;
(2)若存在实数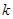 ,使得关于
,使得关于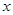 的方程
的方程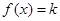 在
在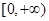 上有两个不相等的实数根,求
上有两个不相等的实数根,求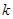 的取值范围.
的取值范围.
(本小题满分10分)
求值: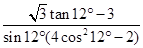 .
.
已知函数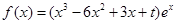 ,
, .
.
(1)若函数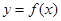 依次在
依次在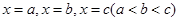 处取到极值.
处取到极值.
①求 的取值范围;
的取值范围;
②若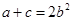 ,求
,求 的值.
的值.
(2)若存在实数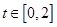 ,使对任意的
,使对任意的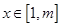 ,不等式
,不等式 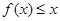 恒成立.求正整数
恒成立.求正整数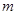 的最大值
的最大值
如图,在直角坐标系中,O为坐标原点,直线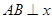 轴于点
轴于点 ,
, 动点
动点 到直线
到直线 的距离是它到点
的距离是它到点 的距离的2倍.
的距离的2倍.
(I)求点 的轨迹方程;
的轨迹方程;
(II)设点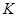 为点
为点 的轨迹与
的轨迹与 轴正半轴的交点,直线
轴正半轴的交点,直线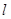 交点
交点 的轨迹于
的轨迹于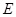 ,
,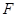 两点(
两点(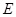 ,
,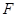 与点
与点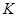 不重合),且满足
不重合),且满足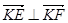 ,动点
,动点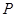 满足
满足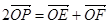 ,求直线
,求直线 的斜率的取值范围.
的斜率的取值范围.
已知数列 满足
满足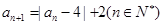 .
.
(1)若 ,求
,求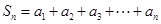 ;
;
(2)试探求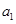 的值,使得数列
的值,使得数列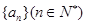 成等差数列.
成等差数列.
如图,在三棱柱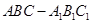 中,侧面
中,侧面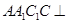 底面
底面 ,
,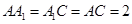 ,
,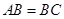 ,且
,且 为
为 中点.
中点.
(I)证明: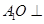 平面
平面 ;
;
(II)求直线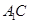 与平面
与平面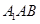 所成角的正弦值;
所成角的正弦值;
(III)在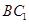 上是否存在一点
上是否存在一点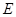 ,使得
,使得 平面
平面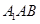 ,若不存在,说明理由;若存在,确定点
,若不存在,说明理由;若存在,确定点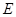 的位置.
的位置.