如图，二次函数y=
x2+bx+c的图象与x轴交于A（3，0），B（–1，0），与y轴交于点C．若点P，Q同时从A点出发，都以每秒1个单位长度的速度分别沿AB，AC边运动，其中一点到达端点时，另一点也随之停止运动．
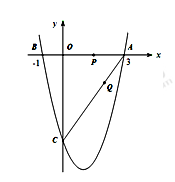
（1）求该二次函数的解析式及点C的坐标；
（2）当P，Q运动t秒时，△APQ沿PQ翻折，点A恰好落在抛物线上D点处，请判定此时四边形APDQ的形状并求说明理由．
（3）当点P运动到B点时，点Q停止运动，这时，在x轴上是否存在点E，使得以A，E，Q为顶点的三角形为等腰三角形？若存在，请求出E点坐标；若不存在，请说明理由
如图,在平行四边形ABCD中,点E,F分别是AB,CD的中点.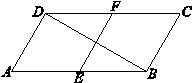
(1)求证：四边形AEFD是平行四边形；(2)若∠A=60°,AB=2AD=4,求BD的长.
解下列方程
（1）x(2x―5)=2(2x―5)（2）2x2―3x ―1=0（用配方法）
计算或化简求值
（1）
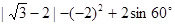
（2）先化简：
,其中
已知，关于x的二次函数，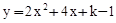
（k为正整数）.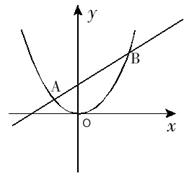
（1）若二次函数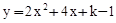的图象与x轴有两个交点，求k的值.
（2）若关于x的一元二次方程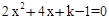
（k为正整数）有两个不相等的整数解，点A（m，y1），B（m+1，y2），C（m+2，y3）都在二次函数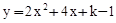（k为正整数）图象上，求使y1≤y2≤y3成立的m的取值范围.
（3）将（2）中的抛物线平移，当顶点至原点时，直线y=2x+b交抛物线于A(-1，n)、B(2，t)两点，问在y轴上是否存在一点C，使得△ABC的内心在y轴上.若存在，求出点C的坐标；若不存在，请说明理由.
如图，在⊙O中，AB为⊙O的直径，AC为弦，OC=4，∠OAC=60°.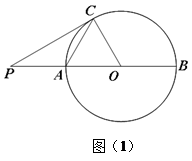
（1）求∠AOC的度数；
（2）在图（1）中，P为直径BA的延长线上一点，且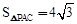
，求证：PC为⊙O的切线.
（3）如图（2），一动点M从A点出发，在⊙O上按逆时针方向运动一周（点M不与点C重合），当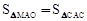
时，求动点M所经过的弧长.