（本小题满分12分）已知关于
的一元二次函数
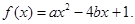
（1）若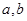
分别表示将一枚质地均匀的骰子先后抛掷两次时第一次、第二次正面朝上出现的点数，求满足函数
在区间[
上是增函数的概率；
（2）设点（
，
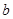）是区域
内的随机点，求函数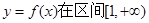
上是增函数的概率.
已知
，
，
．
（1）求
的值；
（2）求
的值．
已知指数函数
满足：
，定义域为
的函数
是奇函数．
（1）确定
和的解析式；
（2）判断函数
的单调性，并用定义证明；
（3）若对于任意
，都有
成立，求
的取值范围．
某种商品在
天内每件的销售价格
（元）与时间
（天）的函数关系用如图表示，该商品在天内日销售量
（件）与时间（天）之间的关系如下表：
（1）根据提供的图象（如图），写出该商品每件的销售价格与时间的函数关系式；
（2）根据表
提供的数据，写出日销售量与时间的一次函数关系式；
（3）求该商品的日销售金额的最大值，并指出日销售金额最大的一天是天中的第几天．（日销售金额
每件的销售价格
日销售量）
设
．
（1）若
，判断并证明函数
的奇偶性；
（2）令
，
，当
取何值时
取得最小值，最小值为多少？
若
是定义在
上的增函数，且对一切
，
，满足
．
（1）求
的值；
（2）若
，解不等式
．