设 .
.
(1)若 ,判断并证明函数
,判断并证明函数 的奇偶性;
的奇偶性;
(2)令 ,
, ,当
,当 取何值时
取何值时 取得最小值,最小值为多少?
取得最小值,最小值为多少?
(本小题满分12分)
已知函数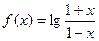 (Ⅰ)求证:对于
(Ⅰ)求证:对于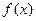 的定义域内的任意两个实数
的定义域内的任意两个实数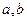 ,都有
,都有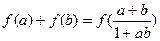 ;(Ⅱ)判断
;(Ⅱ)判断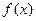 的奇偶性,并予以证明.
的奇偶性,并予以证明.
(本小题满分12分)
已知集合A={x|x2-3x+2=0},B={x|x2-mx+2=0},且A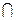 B=B,求实数m的取值范围。
B=B,求实数m的取值范围。
(本小题满分10分)
已知直线l经过点P(1,1),倾斜角 .
.
(Ⅰ)写出直线l的参数方程
(Ⅱ)设l与圆x2+y2=4相交与两点A、B,求点P到A、B两点的距离之积.
(本小题满分10分)
已知函数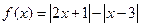 .
.
(Ⅰ)解不等式 ≤4;
≤4;
(Ⅱ)若存在x使得 ≤0成立,求实数a的取值范围.
≤0成立,求实数a的取值范围.
(本小题满分10分)
如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD∥MN,AC与BD相交于点E.
(Ⅰ)求证:△ABE≌△ACD;
(Ⅱ)若AB=6,BC=4,求AE.