(本小题满分12分)已知函数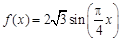 在同一半周期内的图象过点
在同一半周期内的图象过点 ,其中
,其中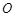 为坐标原点,
为坐标原点, 为函数
为函数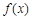 图象的最高点,
图象的最高点,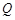 为函数
为函数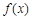 的图象与
的图象与 轴的正半轴的交点.
轴的正半轴的交点.
(Ⅰ)试判断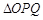 的形状,并说明理由.
的形状,并说明理由.
(Ⅱ)若将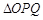 绕原点
绕原点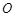 按逆时针方向旋转角
按逆时针方向旋转角 时,顶点
时,顶点 恰好同时落在曲线
恰好同时落在曲线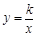
 上(如图所示),求实数
上(如图所示),求实数 的值.
的值.
在△ 中,三个内角
中,三个内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,且
,且 .
.
(1) 求角 ;
;
(2) 若△ 的面积
的面积 ,
, ,求
,求 的值.
的值.
已知等比数列 的各项均为正数,且
的各项均为正数,且 ,
, .
.
(1) 求数列 的通项公式;
的通项公式;
(2) 设 ,求数列
,求数列 的前
的前 项和
项和 .
.
已知函数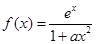 ,其中
,其中 为实数,常数
为实数,常数 .
.
(1) 若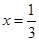 是函数
是函数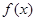 的一个极值点,求
的一个极值点,求 的值;
的值;
(2) 当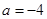 时,求函数
时,求函数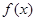 的单调区间;
的单调区间;
(3) 当 取正实数时,若存在实数
取正实数时,若存在实数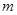 ,使得关于
,使得关于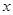 的方程
的方程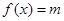 有三个实数根,求
有三个实数根,求 的取值范围.
的取值范围.
如图,椭圆
 的左焦点为
的左焦点为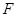 ,过点
,过点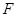 的直线交椭圆于
的直线交椭圆于 两点.
两点. 的最大值是
的最大值是 ,
, 的最小值是
的最小值是 ,满足
,满足 .
.
(1) 求该椭圆的离心率;
(2) 设线段 的中点为
的中点为 ,
, 的垂直平分线与
的垂直平分线与 轴和
轴和 轴分别交于
轴分别交于 两点,
两点, 是坐标原点.记
是坐标原点.记 的面积为
的面积为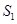 ,
,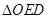 的面积为
的面积为 ,求
,求 的取值范围.
的取值范围.
如图所示几何体是正方体 截去三棱锥
截去三棱锥 后所得,点
后所得,点 为
为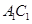 的中点.
的中点.
(1) 求证:平面 平面
平面 ;
;
(2) 求平面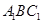 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.