(本小题满分12分)已知在平面直角坐标系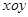 中,椭圆
中,椭圆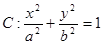 ,长半轴长为4,离心率为
,长半轴长为4,离心率为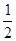 ,
,
(1)求椭圆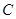 的标准方程;
的标准方程;
(2)若点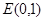 ,问是否存在直线
,问是否存在直线 与椭圆交于
与椭圆交于 两点且
两点且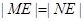 ,若存在,求出直线
,若存在,求出直线 斜率的取值范围;若不存在,请说明理由.
斜率的取值范围;若不存在,请说明理由.
(本小题满分14分)已知复数 ,
,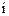 为虚数单位,
为虚数单位,
(1)当复数 纯虚数,求
纯虚数,求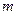 的值;
的值;
(2)当复数 在复平面上的对应点位于第二、四象限角平分线上,求
在复平面上的对应点位于第二、四象限角平分线上,求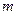 的值.
的值.
(3)若 ,求
,求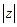
(本小题满分12 分)
已知函数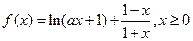 ,其中
,其中 ;
;
(1)若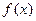 在x=1处取得极值,求
在x=1处取得极值,求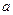 的值;
的值;
(2)求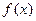 的单调区间;
的单调区间;
(3)若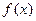 的最小值为1,求
的最小值为1,求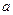 的取值范围。
的取值范围。
(本小题满分12 分)
已知函数f(x)= 的定义域为R,且
的定义域为R,且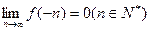 ;
;
(1)求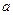 与
与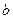 的取值范围;
的取值范围;
(2)若f(1)= ,且f(x)在[0,1]上的最小值为,求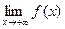 的值。
的值。
(本小题满分12 分)
已知函数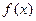 是定义在R上的不恒为零的函数,且对于任意的
是定义在R上的不恒为零的函数,且对于任意的 、
、 ∈R,都满足
∈R,都满足 ,若
,若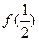 =1,
=1,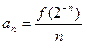 ;
;
(1)求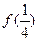 、
、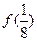 、
、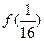 的值;
的值;
(2)猜测数列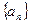 的通项公式,并用数学归纳法证明。
的通项公式,并用数学归纳法证明。
(本小题满分12分)
设f(x)是定义在[-1,1]上的奇函数,对于任意的
 当
当 时,都
时,都
有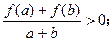
(1)若函数g(x)=f(x-c)和h(x)=f(x-c2)的定义域的交集是空集,求c的取值范围;
(2)判断函数f(x)在[-1,1]上的单调性,并用定义证明。