衡阳市八中对参加“社会实践活动”的全体志愿者进行学分考核,因该批志愿者表现良好,学校决定考核只有合格和优秀两个等次.若某志愿者考核为合格,授予1个学分;考核为优秀,授予2个学分,假设该校志愿者甲、乙、丙考核为优秀的概率分别为 、
、 、
、 ,他们考核所得的等次相互独立.
,他们考核所得的等次相互独立.
(1)求在这次考核中,志愿者甲、乙、丙三人中至少有一名考核为优秀的概率;
(2)记在这次考核中甲、乙、丙三名志愿者所得学分之和为随机变量 ,求随机变量
,求随机变量 的分布列及数学期望.
的分布列及数学期望.
(本小题满分12分)设函数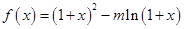 ,
, .
.
(1)当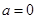 时,
时,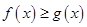 在
在 上恒成立,求实数
上恒成立,求实数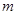 的取值范围;
的取值范围;
(2)当 时,若函数
时,若函数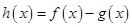 在
在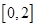 上恰有两个不同的零点,求实数
上恰有两个不同的零点,求实数 的取值范围;
的取值范围;
(3)是否存在常数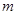 ,使函数
,使函数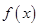 和函数
和函数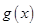 在公共定义域上具有相同的单调性?若存在,求出
在公共定义域上具有相同的单调性?若存在,求出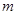 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(本小题满分12分)已知函数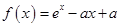 ,其中
,其中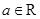 ,
,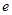 为自然对数底数.
为自然对数底数.
(1)讨论函数 的单调性,并写出相应的单调区间;
的单调性,并写出相应的单调区间;
(2)设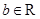 ,若函数
,若函数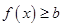 对任意
对任意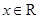 都成立,求
都成立,求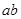 的最大值.
的最大值.
(本小题满分12分)已知函数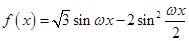 (
(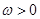 )的最小正周期为
)的最小正周期为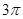 .
.
(1)求函数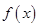 在区间
在区间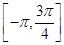 上的最大值和最小值;
上的最大值和最小值;
(2)在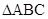 中,
中,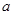 ,
, ,
,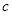 分别为角
分别为角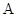 ,
, ,
,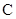 所对的边,且
所对的边,且 ,
, ,求角
,求角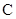 的大小;
的大小;
(3)在(2)的条件下,若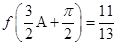 ,求
,求 的值.
的值.
(本小题满分12分)已知角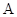 ,
,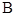 ,
,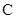 是
是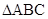 的三个内角,
的三个内角,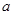 ,
,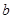 ,
,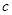 是各角的对边,若向量
是各角的对边,若向量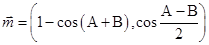 ,
,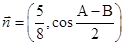 ,且
,且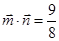 .
.
(1)求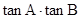 的值;
的值;
(2)求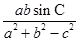 的最大值.
的最大值.
(本小题满分10分)设数列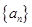 满足
满足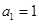 ,
,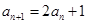 .
.
(1)求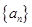 的通项公式;
的通项公式;
(2)记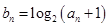 ,求数列
,求数列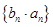 的前
的前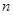 项和
项和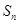 .
.