如图①,一条宽为1km的两平行河岸有三个工厂 、
、 、
、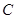 ,工厂
,工厂 与
与 、
、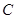 的直线距离都是2km,
的直线距离都是2km, 与河岸垂直,
与河岸垂直,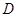 为垂足.现要在河岸
为垂足.现要在河岸 上修建一个供电站,并计划铺设地下电缆和水下电缆,从供电站向三个工厂供电.已知铺设地下电缆、水下电缆的费用分别为2万元/km、4万元/km.
上修建一个供电站,并计划铺设地下电缆和水下电缆,从供电站向三个工厂供电.已知铺设地下电缆、水下电缆的费用分别为2万元/km、4万元/km.
(Ⅰ)已知工厂 与
与 之间原来铺设有旧电缆(原线路不变),经改造后仍可使用,旧电缆的改造费用是0.5万元/km.现决定将供电站建在点
之间原来铺设有旧电缆(原线路不变),经改造后仍可使用,旧电缆的改造费用是0.5万元/km.现决定将供电站建在点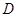 处,并通过改造旧电缆修建供电线路,试求该方案总施工费用的最小值;
处,并通过改造旧电缆修建供电线路,试求该方案总施工费用的最小值;
(Ⅱ)如图②,已知供电站建在河岸 的点
的点 处,且决定铺设电缆的线路为
处,且决定铺设电缆的线路为 、
、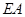 、
、 ,若
,若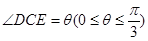 ,试用
,试用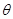 表示出总施工费用
表示出总施工费用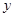 (万元)的解析式,并求总施工费用
(万元)的解析式,并求总施工费用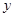 的最小值.
的最小值.
(本小题满分12分,(Ⅰ)小问4分,(Ⅱ)小问8分)
已知动点 到直线
到直线
 的距离是它到点
的距离是它到点 的距离的
的距离的 倍.
倍.
(Ⅰ)求动点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)设轨迹 上一动点
上一动点 满足:
满足: ,其中
,其中 是轨迹
是轨迹 上的点,直线
上的点,直线 与
与 的斜率之积为
的斜率之积为 ,若
,若 为一动点,
为一动点, 为两定点,
为两定点, .
.
(本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分)
已知一家公司生产某种品牌服装的年固定成本为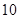 万元,每生产
万元,每生产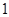 千件需另投入
千件需另投入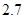 万元.设该公司一年内生产该品牌服装
万元.设该公司一年内生产该品牌服装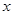 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为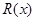 万元,且
万元,且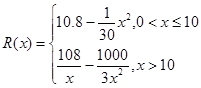
(Ⅰ)写出年利润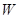 (万元)关于年产量
(万元)关于年产量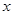 (千件)的函数解析式;
(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该公司在这一品牌服装的生产中所获得的年利润最大,并求出最大年利润.(注:年利润=年销售收入-年总成本).
(本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分)
在如图所示的多面体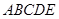 中,
中,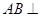 平面
平面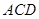 ,
, 平面
平面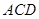 ,
,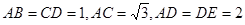 ,
,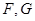 为
为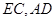 的中点.
的中点.
(Ⅰ)求证: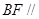 平面
平面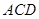 ;
;
(Ⅱ)求三棱锥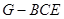 的体积.
的体积.
(本小题满分13分,(Ⅰ)小问5分,(Ⅱ)小问8分)
设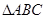 的内角
的内角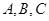 的对边分别为
的对边分别为 ,
,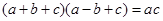 .
.
(Ⅰ)求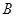 ;
;
(Ⅱ)若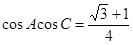 ,求
,求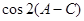 .
.
(本小题满分13分,(Ⅰ)小问6分,(Ⅱ)小问3分,(Ⅲ)小问4分)
为了了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,记录了小李第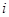 天打篮球的时间
天打篮球的时间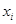 (单位:小时)与当天投篮命中率
(单位:小时)与当天投篮命中率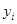 的数据,其中
的数据,其中 .
.
算得: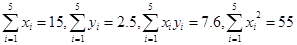 .
.
(Ⅰ)求投篮命中率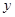 对打篮球时间
对打篮球时间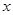 的线性回归方程
的线性回归方程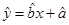 ;
;
(Ⅱ)判断变量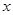 与
与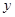 之间是正相关还是负相关;
之间是正相关还是负相关;
(Ⅲ)若小李明天准备打球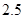 小时,预测他的投篮命中率.
小时,预测他的投篮命中率.
附:线性回归方程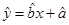 中
中 ,其中
,其中 为样本平均数.
为样本平均数.