若椭圆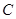 的方程为
的方程为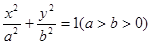 ,
, 、
、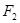 是它的左、右焦点,椭圆
是它的左、右焦点,椭圆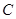 过点
过点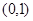 ,且离心率为
,且离心率为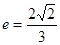 .
.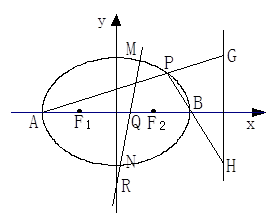
(Ⅰ)求椭圆的方程;
(Ⅱ)设椭圆的左右顶点为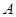 、
、 ,直线
,直线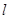 的方程为
的方程为 ,
,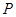 是椭圆上任一点,直线
是椭圆上任一点,直线 、
、 分别交直线
分别交直线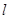 于
于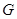 、
、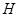 两点,求
两点,求 的值;
的值;
(Ⅲ)过点 任意作直线
任意作直线 (与
(与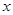 轴不垂直)与椭圆
轴不垂直)与椭圆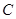 交于
交于 、
、 两点,与
两点,与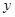 轴交于
轴交于 点
点 ,
, .证明:
.证明: 为定值.
为定值.
已知函数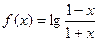
(1)求函数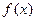 的定义域;
的定义域;
(2)判断函数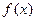 的单调性,并简要说明理由,不需要用定义证明
的单调性,并简要说明理由,不需要用定义证明
(1)已知集合A={x|  }, B="{x|" 2<x<10},求
}, B="{x|" 2<x<10},求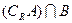 ;
;
(2)化解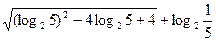
设集合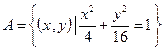 ,
,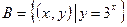 ,则
,则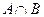 的子集的个数是()
的子集的个数是()
| A.4 | B.3 | C.2 | D.1 |
(本小题满分14分)
设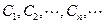 是坐标平面上的一列圆,它们的圆心都在
是坐标平面上的一列圆,它们的圆心都在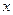 轴的正半轴上,且都与直线
轴的正半轴上,且都与直线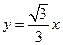 相切,对每一个正整数
相切,对每一个正整数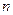 ,圆
,圆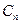 都与圆
都与圆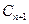 相互外切,以
相互外切,以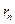 表示
表示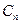 的半径,已知
的半径,已知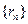 为递增数列.
为递增数列.
(1)证明: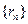 为等比数列;
为等比数列;
(2)设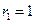 ,求数列
,求数列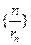 的前
的前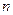 项和.
项和.
(本小题满分14分)
已知A(1,1)是椭圆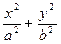 =1(
=1(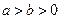 )上一点,
)上一点,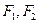 是椭圆的两焦点,且满足
是椭圆的两焦点,且满足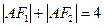 .
.
(1)求椭圆的标准方程;
(2)设点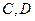 是椭圆上两点,直线
是椭圆上两点,直线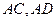 的倾斜角互补,求直线
的倾斜角互补,求直线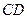 的斜率.
的斜率.