(本小题满分12分)已知函数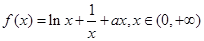 (a是实数),
(a是实数),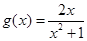 +1。
+1。
(1)若函数f(x)在[1,+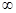 )上是单调函数,求a的取值范围;
)上是单调函数,求a的取值范围;
(2)是否存在正实数a满足:对于任意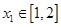 ,总存在
,总存在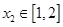 ,使得f(x1)=g(x2)成立,若存在求出a的范围,若不存在,说明理由。
,使得f(x1)=g(x2)成立,若存在求出a的范围,若不存在,说明理由。
(3)若数列 满足
满足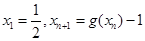 ,求证:
,求证: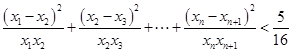 。
。
(本小题满分14分)
如图(1),在直角梯形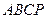 中,
中,
 、
、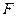 、
、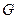 分别是线段
分别是线段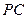 、
、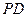 、
、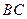 的中点,现将
的中点,现将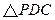 折起,使平面
折起,使平面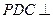 平面
平面 (如图(2)).
(如图(2)).
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)取 中点为
中点为 ,求证:
,求证:  平面
平面 ,
,
(本小题满分12分)过原点且斜率为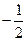 的直线
的直线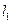 与直线
与直线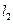 :2x + 3y -1=0交于
:2x + 3y -1=0交于 点,求过点
点,求过点 且圆心在直线
且圆心在直线 上,并与直线
上,并与直线 相切的圆的方程。
相切的圆的方程。
(本小题满分12分)设向量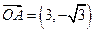 ,
,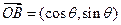 ,其中
,其中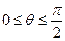 .
.
(1)若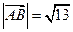 ,求
,求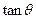 的值;
的值;
(2)求△ 面积的最大值.
面积的最大值.
(本小题12分)函数的性质通常指函数的定义域、值域、奇偶性、周期性、单调性等,请选择适当的探究顺序,研究函数f(x)= 的性质,并在此基础上,作出其在
的性质,并在此基础上,作出其在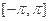 上的图像.
上的图像.
(本小题10分)设向量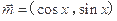 ,
, ,
,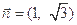 .
.
(Ⅰ)若 ,求
,求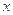 的值;
的值;
(Ⅱ)设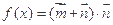 ,求函数
,求函数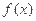 的值域.
的值域.