如图,在四棱台ABCD-A1B1C1D1中,DD1 平面ABCD,底面ABCD是平行四边形,AB=AD=2A1B1,
平面ABCD,底面ABCD是平行四边形,AB=AD=2A1B1,

(1)证明:BB1 AC;
AC;
(2)若AB=2,且二面角A1-AB-C大小为60 ,连接AC,BD,设交点为O,连接B1O。求三棱锥B1-ABO外接球的体积。(球体体积公式:
,连接AC,BD,设交点为O,连接B1O。求三棱锥B1-ABO外接球的体积。(球体体积公式: ,R是球半径)
,R是球半径)
已知A、B分别是椭圆 的左右两个焦点,O为坐标原点,点P
的左右两个焦点,O为坐标原点,点P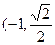 )在椭圆上,线段PB与y轴的交点M为线段PB的中点。
)在椭圆上,线段PB与y轴的交点M为线段PB的中点。
(1)求椭圆的标准方程;
(2)点C是椭圆上异于长轴端点的任意一点,对于△ABC,求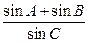 的值。
的值。
已知椭圆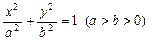 与过点A(2,0),B(0,1)的直线l有且只有一个公共点T,且椭圆的离心率
与过点A(2,0),B(0,1)的直线l有且只有一个公共点T,且椭圆的离心率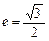 .求椭圆方程
.求椭圆方程
如图,在Rt△ABC中,∠CAB=90°,AB=2,AC= 。一曲线E过点C,动点P在曲线E上运动,且保持|PA|+|PB|的值不变,直线l经过A与曲线E交于M、N两点。
。一曲线E过点C,动点P在曲线E上运动,且保持|PA|+|PB|的值不变,直线l经过A与曲线E交于M、N两点。
(1)建立适当的坐标系,求曲线E的方程;
(2)设直线l的斜率为k,若∠MBN为钝角,求k的取值范围。
已知椭圆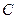 的中心为坐标原点
的中心为坐标原点 ,一个长轴端点为
,一个长轴端点为 ,短轴端点和焦点所组成的四边形为正方形,直线
,短轴端点和焦点所组成的四边形为正方形,直线 与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且
与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且 .
.
(1)求椭圆方程;
(2)求m的取值范围.
 是椭圆
是椭圆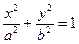 上一点,
上一点,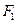 、
、 是椭圆的两个焦点,求
是椭圆的两个焦点,求 的最大值与最小值
的最大值与最小值