（本小题满分12分）已知函数f（x）＝
sinxcosx－3cos2x＋
（1）求函数f（x）的最小正周期及单调递增区间；
（2）△ABC的内角A，B，C的对边分别是a，b，c，若
，b＝1，c＝，且a＞b，试判断△ABC的形状，并说明理由.
已知函数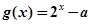
的值域为集合A，函数
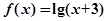的定义域为集合B．
（1）求集合A，B；
（2）若集合A，B满足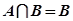
，求实数a的取值范围．
某工厂在试验阶段大量生产一种零件，这种零件有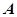
、
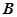两项技术指标需要检测，设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为
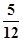，至少一项技术指标达标的概率为
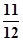．按质量检验规定：两项技术指标都达标的零件为合格品．
（1）求一个零件经过检测为合格品的概率是多少？
（2）任意依次抽取该种零件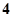
个，设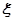
表示其中合格品的个数，求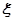的分布列及数学期望
．
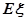有甲、乙两个班进行数学考试，按照大于或等于85分为优秀，85分以下为非优秀统计成绩后，得到如下的2×2列联表：
| 优秀 |
非优秀 |
总计 |
|
| 甲班 |
20 |
||
| 乙班 |
60 |
||
| 总计 |
210 |
已知从全部210人中随机抽取1人为优秀的概率为
．
（1）请完成上面的2×2列联表；
（2）根据列联表的数据，若按99%的可靠性要求，能否认为“成绩与班级有关系”．
附：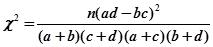
，其中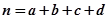
.
| 参考数据 |
当 ≤2.706时，无充分证据判定变量A，B有关联，可以认为两变量无关联； |
| 当＞2.706时，有90%的把握判定变量A，B有关联； |
|
| 当＞3.841时，有95%的把握判定变量A，B有关联； |
|
| 当＞6.635时，有99%的把握判定变量A，B有关联． |
一个袋中装有8个大小质地相同的球，其中4个红球、4个白球，现从中任意取出四个球，设
为取得红球的个数．
（1）求的分布列；
（2）若摸出4个都是红球记5分，摸出3个红球记4分，否则记2分．求得分的期望．
证明：在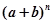
的展开式中，奇数项的二项式系数的和等于偶数项的二项式系数的和.