（本小题满分12分）已知函数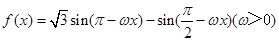
的图像上两相邻最高点的坐标分别为
．
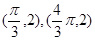（Ⅰ）求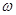
的值；
（Ⅱ）在△ABC中，a,b,c分别是角A,B,C的对边，且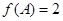
求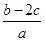
的取值范围。
一次函数
是
上的增函数，
，已知
．
（1）求；
（2）若
在
单调递增，求实数
的取值范围；
（3）当
时，有最大值
，求实数的值．
已知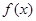
是定义在
上的奇函数，当
时，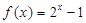
．
（1）求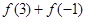
；
（2）求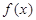
的解析式；
（3）若
，求区间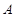
．
已知函数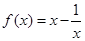
．
（1）用函数单调性的定义证明：函数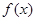
在区间
上为增函数；
（2）若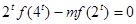
，当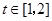
时，求实数m的取值范围．
如图所示，已知S是正三角形ABC所在平面外的一点，且SA=SB=SC，SG为△SAB上的高，D、E、F分别是AC、BC、SC的中点，试判断SG与平面DEF的位置关系，并给予证明．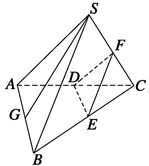
己知圆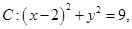
直线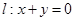
．
（1）求与圆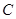
相切，且与直线
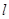平行的直线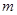
的方程；
（2）若直线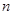
与圆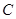有公共点，且与直线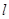垂直，求直线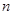在
轴上的截距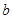
的取值范围．