(本小题满分12分)设函数 .
.
(Ⅰ)当 时,求
时,求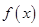 的极值;
的极值;
(Ⅱ)设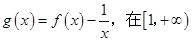 上单调递增,求
上单调递增,求 的取值范围;
的取值范围;
(Ⅲ)当 时,求
时,求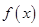 的单调区间.
的单调区间.
求下列函数的导数:
(1)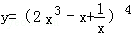 ;
;
(2) ;
;
(3)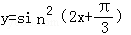 ;
;
(4)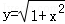 .
.
求下列函数的导数:
(1)y=x12;
(2)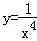 ;
;
(3)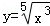 .
.
已知空间直角坐标系O﹣xyz中的点A(1,1,1),平面α过点A且与直线OA垂直,动点P(x,y,z)是平面α内的任一点.
(1)求点P的坐标满足的条件;
(2)求平面α与坐标平面围成的几何体的体积.
在空间直角坐标系中,解答下列各题:
(1)在x轴上求一点P,使它与点P0(4,1,2)的距离为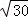 ;
;
(2)在xOy平面内的直线x+y=1上确定一点M,使它到点N(6,5,1)的距离最小.
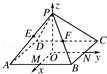
如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.