福州市出租车因车型不同,收费标准也不同。A型车的起步价10元(3km以内收费10元),3km 后每千米收费1.2元;B 型车的起步价8元(3km以内收费8元),3km 后每千米 收费1.4元.
(1)请分别计算乘坐A型车与B型车行走xkm(x>3)各需付多少元(列代数式);
(2)若张老师要乘出租车到20km处的省体育中心,从节省费用的角度出发,张老师应乘坐哪种型号的车?
某中学组织全校3200名学生进行了“法律法规”相关知识竞赛.为了解本次知识竞赛的成绩情况,从中随机抽取了部分学生的成绩(得分取正整数,满分为100分),并绘制了如图的频数分布表和频数分布直方图.
| 分组 |
频数 |
频率 |
| 50.5~60.5 |
m |
0.05 |
| 60.5~70.5 |
a |
b |
| 70.5~80.5 |
80 |
n |
| 80.5~90.5 |
104 |
0.26 |
| 90.5~100.5 |
148 |
0.37 |
| 合计 |
1 |
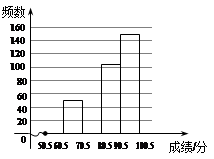
请根据以上提供的信息,解答下列问题:
(1)则a=,b=,并补全频数分布直方图;
(2)上述学生成绩的中位数落在哪一组范围内?
(3)学校将对成绩在90.5~100.5分之间的学生进行奖励,请估计全校3 200名学生中约有多少名获奖?
如图已知四边形ABCD是平行四边形,AC与BD相交于O点,且BC⊥AC,AB=8,∠ABC=30°,
(1)求AD和BD的长;
(2)求平行四边形ABCD的面积.
解方程:(1) ;(2)
;(2) .
.
计算:(1) ;(2)
;(2) .
.
如图,在平面直角坐标系中,坐标原点为O,A点坐标为(4,0),B点坐标为(﹣1,0),以AB的中点P为圆心,AB为直径作⊙P的正半轴交于点C.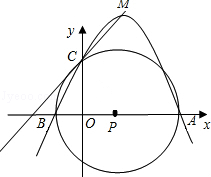
(1)求经过A、B、C三点的抛物线所对应的函数解析式;
(2)设M为(1)中抛物线的顶点,求直线MC对应的函数解析式;
(3)试说明直线MC与⊙P的位置关系,并证明你的结论.