某中学组织全校3200名学生进行了“法律法规”相关知识竞赛．为了解本次知识竞赛的成绩情况，从中随机抽取了部分学生的成绩（得分取正整数，满分为100分），并绘制了如图的频数分布表和频数分布直方图．
| 分组 |
频数 |
频率 |
| 50.5~60.5 |
m |
0.05 |
| 60.5~70.5 |
a |
b |
| 70.5~80.5 |
80 |
n |
| 80.5~90.5 |
104 |
0.26 |
| 90.5~100.5 |
148 |
0.37 |
| 合计 |
|
1 |
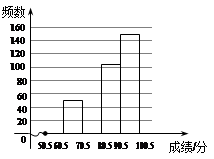
请根据以上提供的信息，解答下列问题：
（1）则a= ，b= ，并补全频数分布直方图；
（2）上述学生成绩的中位数落在哪一组范围内？
（3）学校将对成绩在90.5~100.5分之间的学生进行奖励，请估计全校3 200名学生中约有多少名获奖？
先化简，再求值：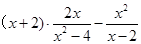
，其中
．
解方程：
（9分计算：
如图，是反比例函数
和
（k1＞k2）在第一象限的图象，直线
∥
轴，并分别交两条曲线于、两点。
（1）若点的纵坐标是
，则可得点的纵坐标是．
（2）若
，则
与
之间的关系是．
（本小题满分14分）根据下列要求，解答相关问题.
（1）请补全以下求不等式
的解集的过程.
①构造函数，画出图象：根据不等式特征构造二次函数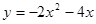
；并在下面的坐标系中(见图1)画出二次函数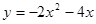的图象（只画出图象即可）.
②求得界点，标示所需：当y=0时，求得方程
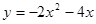的解为；并用锯齿线标示出函数图象中y≥0的部分.
③借助图象，写出解集：由所标示图象，可得不等式的解集为.
（2）利用（1）中求不等式解集的步骤，求不等式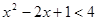
的解集.
①构造函数，画出图象：
②求得界点，标示所需：
③借助图像，写出解集：
（3）参照以上两个求不等式解集的过程，借助一元二次方程的求根公式，直接写出关于x的不等式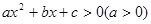
的解集.
