本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
(1)数列 各项均不为0,前n项和为
各项均不为0,前n项和为 ,
, ,
, 的前n项和为
的前n项和为 ,且
,且 ,若数列
,若数列 共3项,求所有满足要求的数列;
共3项,求所有满足要求的数列;
(2)求证: 是满足已知条件的一个数列;
是满足已知条件的一个数列;
(3)请构造出一个满足已知条件的无穷数列 ,并使得
,并使得 ;若还能构造其他符合要求的数列,请一并写出(不超过四个)。
;若还能构造其他符合要求的数列,请一并写出(不超过四个)。
已知函数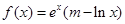 (m为常数,e=2.71828…是自然对数的底数),函数
(m为常数,e=2.71828…是自然对数的底数),函数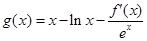 的最小值为1,其中
的最小值为1,其中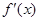 是函数f(x)的导数.
是函数f(x)的导数.
(1)求m的值.
(2)判断直线y=e是否为曲线f(x)的切线,若是,试求出切点坐标和函数f(x)的单调区间;若不是,请说明理由.
某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:
| 分数段 |
[50,70) |
[70,90) |
[90,110) |
[110,130) |
[130,150) |
总计 |
| 频数 |
b |
|||||
| 频率 |
a |
0.25 |

(1)求表中a,b的值及分数在[90,100)范围内的学生人数,并估计这次考试全校学生数学成绩的及格率(分数在[90,150)内为及格):
(2)从成绩大于等于110分的学生中随机选两人,求这两人成绩的平均分不小于130分的概率.
如图,在四棱锥A-BCDE中,侧面∆ADE是等边三角形,底面BCDE是等腰梯形,且CD∥BE,DE=2,CD=4,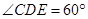 ,M是DE的中点,F是AC的中点,且AC=4,
,M是DE的中点,F是AC的中点,且AC=4,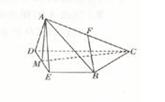
求证:(1)平面ADE⊥平面BCD;
(2)FB∥平面ADE.
已知函数 的图象过点(0,
的图象过点(0, ),最小正周期为
),最小正周期为 ,且最小值为-1.
,且最小值为-1.
(1)求函数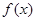 的解析式.
的解析式.
(2)若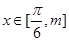 ,
,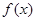 的值域是
的值域是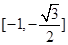 ,求m的取值范围.
,求m的取值范围.
等差数列{am}的前m项和为Sm,已知S3=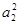 ,且S1,S2,S4成等比数列,
,且S1,S2,S4成等比数列,
(1)求数列{am}的通项公式.
(2)若{am}又是等比数列,令bm= ,求数列{bm}的前m项和Tm.
,求数列{bm}的前m项和Tm.