(本小题满分12分)某创业投资公司拟投资开发某种新能源产品,估计能获得投资收益的范围是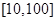 (单位:万元).现准备制定一个对科研课题组的奖励方案:奖金
(单位:万元).现准备制定一个对科研课题组的奖励方案:奖金 (单位:万元)随投资收益
(单位:万元)随投资收益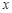 (单位:万元)的增加而增加,且奖金不超过
(单位:万元)的增加而增加,且奖金不超过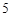 万元,同时奖金不超过投资收益的20%.
万元,同时奖金不超过投资收益的20%.
(Ⅰ)若建立函数模型 制定奖励方案,请你根据题意,写出奖励模型函数应满足的条件;
制定奖励方案,请你根据题意,写出奖励模型函数应满足的条件;
(Ⅱ)现有两个奖励函数模型: ;
;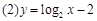 .试分析这两个函数模型是否符合公司要求.
.试分析这两个函数模型是否符合公司要求.
在数列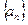 中,已知a1=2,an+1=4an-3n+1,n∈
中,已知a1=2,an+1=4an-3n+1,n∈ .
.
设 ,求证:数列
,求证:数列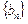 是等比数列;
是等比数列;
某宾馆有相同标准的床位100张,根据经验,当该宾馆的床价(即每张床每天的租金)不超过10元时,床位可以全部租出,当床位高于10元时,每提高1元,将有3张床位空闲.为了获得较好的效益,该宾馆要给床位一个合适的价格,条件是:①要方便结帐,床价应为1元的整数倍;② 该宾馆每日的费用支出为575元,床位出租的收入必须高于支出,而且高出得越多越好.若用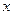 表示床价,用
表示床价,用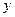 表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入)
表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入)
(1)把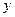 表示成
表示成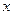 的函数,并求出其定义域;
的函数,并求出其定义域;
(2)试确定该宾馆将床位定价为多少时既符合上面的两个条件,又能使净收入最多?
已知函数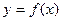 是R上的奇函数且在
是R上的奇函数且在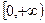 上是增函数,若
上是增函数,若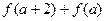 >0, 求
>0, 求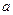 的取值范围
的取值范围
设集合 ,
,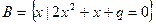 ,若
,若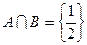 ,求
,求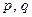 的值及
的值及
在数列{an}中,a1=1,当n≥2时,an,Sn,Sn- 成等比数列.
成等比数列.
(1)求a2,a3,a4,并推出an的表达式;
(2)用数学归纳法证明所得的结论;
(3)求数列{an}所有项的和.