（本题12分）为鼓励居民节约用电，某地试行阶梯电价收费制，具体执行方案如表：
| 档次 |
每户每月用电数（度） |
执行电价（元/度） |
| 第一档 |
小于等于200部分 |
0.5 |
| 第二档 |
大于200小于400部分 |
0.6 |
| 第三档 |
大于等于400部分 |
0.8 |
（1）该地一户居民四月份用电180度，则需缴电费多少元？
（2）某居民八月份用电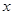
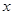度（＞400），用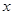的代数式表示该户八月份需交电费多少元？
（3）又一户居民五、六月份共用电500度，缴电费262元．已知该用户六月份用电量大于五月份，且五六月份的用电量均小于400度．问该户居民五、六月份各月用电多少度？
在数学课上,陈老师在黑板上画出如图所示的图形,在△AEC和△DFB中,已知∠E=∠F,点A,B,C,D在同一直线上,并写下三个关系式：①AE∥DF,②AB=CD,③CE=BF．请同学们从中再任意选取两个作为补充条件,剩下的那个关系式作为结论构造命题．小明选取了关系式①,②作为条件,关系式③作为结论.你认为按照小明的选法得到的命题是真命题吗？如果是,请写出证明过程,如果不是,请举出反例．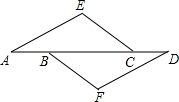
解不等式组：
．
解方程：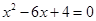
先化简,再求值：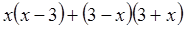
,其中x＝－2．
已知∠AOB=90°，OM是∠AOB的平分线，按以下要求解答问题：
（1）如图1，将三角板的直角顶点P在射线OM上移动，两直角边分别与OA,OB交于点C，D．
①比较大小：PC______PD． (选择“>”或“<”或“=”填空）；
②证明①中的结论．
（2）将三角板的直角顶点P在射线ＯＭ上移动，一直角边与边OA交于点C，且OC=1，另一直角边与直线OB，直线OA分别交于点D，E，当以P，C，E为顶点的三角形与△OCD相似时，试求
的长．（提示：请先在备用图中画出相应的图形，再求的长）. 