如图,直线AB、CD、EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=280,求∠AOG的度数.
先化简,再求值: ,其中a=2-
,其中a=2-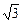
计算:
(本题20分) (湖南湘西,25,20分)如图.抛物线 与x轴相交于点A和点B,与y轴交于点C.
与x轴相交于点A和点B,与y轴交于点C.
(1)求点A、点B和点C的坐标.
(2)求直线AC的解析式.
(3)设点M是第二象限内抛物线上的一点,且 =6,求点M的坐标.
=6,求点M的坐标.
(4)若点P在线段BA上以每秒1个单位长度的速度从A运动(不与B,A重合),同时,点Q在射线AC上以每秒2个单位长度的速度从A 向C运动.设运动的时间为t秒,请求出△APQ的面积S与t的函数关系式,并求出当t为何值时, △APQ的面积最大,最大面积是多少?
向C运动.设运动的时间为t秒,请求出△APQ的面积S与t的函数关系式,并求出当t为何值时, △APQ的面积最大,最大面积是多少?
(本题10分) (湖南湘西24,10分)如图,已知矩形ABCD的两条对角线相交于O,∠ACB=30°,AB=2.
(1)求AC的长.
(2)求∠AOB的度数.
(3)以OB、OC为邻边作菱形OBEC,求菱形OBEC的面积.
(本题8分)(湖南湘西,23,8分)湘西以“椪柑之乡”著称,在椪柑收获季节的某星期天,青山中学抽调八年级(1)、(2)两班部分学生去果园帮助村民采摘椪柑,其中,八年级(1)班抽调男同学2人,女同学8人,共摘得柑840千克;八年级(2)班调男同学4人,女同学6人,共摘得椪柑880千克,问这天被抽调的同学中,男同学每人平均摘椪柑多少千克?女同学每人平均摘椪柑多少千克?