阅读下面材料：
小明观察一个由
正方形点阵组成的点阵图，图中水平与竖直方向上任意两个相邻点间的距离都是1．他发现一个有趣的问题：对于图中出现的任意两条端点在点阵上且互相不垂直的线段，都可以在点阵中找到一点构造垂直，进而求出它们相交所成锐角的正切值．
请回答：（1）如图1，A、B、C是点阵中的三个点，请在点阵中找到点D，作出线段CD，使得CD⊥AB；
（2）如图2，线段AB与CD交于点O．为了求出
的正切值，小明在点阵中找到了点E，连接AE，恰好满足
于F，再作出点阵中的其它线段，就可以构造相似三角形，经过推理和计算能够使问题得到解决．
请你帮小明计算：OC=_______________；
=_______________；
㈠小明在玩积木游戏时，把三个正方形积木摆成一定的形状，正视图如图①，
问题(1)：若此中的三角形△DEF为直角三角形，P的面积为9，Q的面积为15，则M的面积为_______。
问题(2)：若P的面积为36cm2，Q的面积为64 cm2，同时M的面积为100 cm2，则△DEF为_______三角形。
㈡图形变化：如图②，分别以直角三角形的三边为直径向三角形外作三个半圆，你能找出这三个半圆的面积之间有什么关系吗?请说明理由。
我们知道：若x2=9，则x=3或x=－3．
因此，小南在解方程x2+2x－8=0时，采用了以下的方法：
解：移项，得x2+2x=8：
两边都加上l，得x2+2x+1=8+1，所以(x+1) 2=9；
则x+1=3或x+1=－3：
所以x=2或x=－4．
小南的这种解方程方法，在数学上称之为配方法．请用配方法解方程x2－4x－5=0．
如图，有两条公路OM，ON相交成30°，沿公路OM方向离两条公路的交叉处O点80米的A处有一所希望小学，当拖拉机沿ON方向行驶时，路两旁50米内会受到噪音影响，已知有两台相距30米的拖拉机正沿ON方向行驶，它们的速度均为5米/秒，问这两台拖拉机沿ON方向行驶时给小学带来噪音影响的时间是多少？
作图：
（1）在图1中画出△ABC关于点O的中心对称图形。
（2）正方形网格中，每个小正方形的顶点称为格点，以格点为顶点的三角形叫做格点三角形，在图2正方形网格（每个小正方形边长为1）中画出格点△DEF，使DE=DF=5，EF=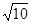
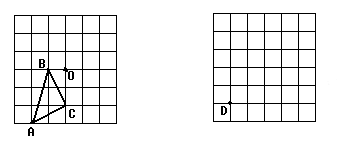
(图1)（图2）
已知：如图，E、F分别是▱ABCD的边AD、BC的中点．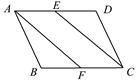
求证：AF＝CE.