已知关于 的方程
的方程 .
.
(1)求证:当 时,方程总有两个不相等的实数根;
时,方程总有两个不相等的实数根;
(2)若二次函数 的图象与x轴交于A,B两点(A在B的左侧),与
的图象与x轴交于A,B两点(A在B的左侧),与 轴交于点C,且tan∠OAC=4,求该二次函数的解析式;
轴交于点C,且tan∠OAC=4,求该二次函数的解析式;
(3)已知点P(m,0)是x轴上的一个动点,过点P作垂直于x轴的直线交(2)中的二次函数图象于点M,交一次函数 的图象于点N.若只有当
的图象于点N.若只有当 时,点M位于点N的下方,求一次函数
时,点M位于点N的下方,求一次函数 的解析式.
的解析式.
如图.抛物线y=x2-4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y="x+" m与对称轴交于点Q.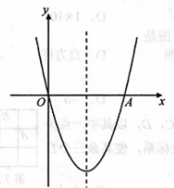
(1)这条抛物线的对称轴是 ,直线PQ与x軸所夹锐角的度数是 ,
(2)若两个三角形面积满足 ,求m的値:
,求m的値:
(3)当点P在x軸下方的抛物线上时.过点C(2,2)的直线AC与直线PQ交于点D,求:
PD+DQ的最大值;②PD DQ的最大值.
DQ的最大值.
已知四边形ABCD内接于⊙O,∠ADC=90°,∠DCB<90°,对角线AC平分∠DCB ,延长DA,CB相交于点E.
(1)如图1,EB=AD,求证:△ABE是等腰直角三角形;
(2)如图2,连接OE,过点E作直线EF,使得∠OEF=30°,当∠ACE≥30°时,判断直线EF与⊙O的位置关系,并说明理由.
图(1)是一个蒙古包的照片,这个蒙古包可以近似看成是圆锥和圆柱组成的几何体,如图(2)所示.
(1)请画出这个几何体的俯视图;
(2)图(3)是这个几何体的正面示意图,已知蒙古包的顶部离地面的高度EO1=6米,圆柱部分的高OO1=4米,底面圆的直径BC=8米,求∠EAO的度数(结果精确到0.1°).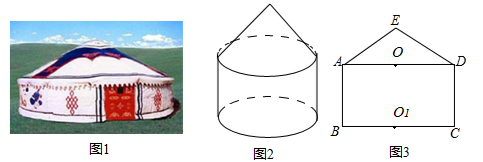
如图,一条河的两岸l1,l2互相平行,在一次综合实践活动中,小颖去测量这条河的宽度,先在对岸l1上选取一个点A,然后在河岸l2时选择点B,使得AB与河岸垂直,接着沿河岸l2走到点C处,测得BC=60米,∠BCA=62°,请你帮小颖算出河宽AB(结果精确到1米).(参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)
某商场经理对某一品牌旅游鞋近一个月的销售情况进行统计后,绘制了如下统计表与条形图: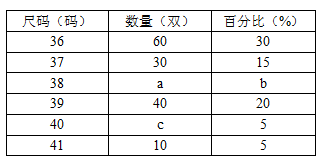
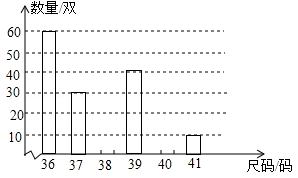
(1)写出表中a,b,c的值;
(2)补全条形图;
(3)商场经理准备购进同一品牌的旅游鞋1500双,请根据市场实际情况估计他应该购进38码的鞋多少双?