问题提出:平面内不在同一条直线上的三点确定一个圆.那么平面内的四点(任意三点均不在同一直线上),能否在同一个圆呢?
初步思考:设不在同一条直线上的三点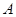 、
、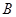 、
、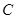 确定的圆为⊙
确定的圆为⊙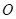 .
.
(1)当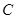 、
、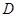 在线段
在线段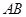 的同侧时,
的同侧时,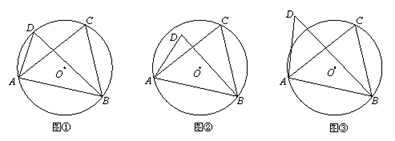
如图①,若点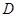 在⊙
在⊙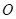 上,此时有
上,此时有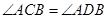 ,理由是 ;
,理由是 ;
如图②,若点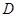 在⊙
在⊙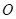 内,此时有
内,此时有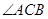
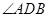 ;
;
如图③,若点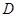 在⊙
在⊙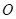 外,此时有
外,此时有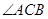
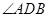 .(填“
.(填“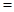 ”、“
”、“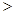 ”或“
”或“ ”);
”);
由上面的探究,请直接写出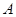 、
、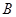 、
、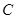 、
、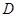 四点在同一个圆上的条件: .
四点在同一个圆上的条件: .
类比学习:(2)仿照上面的探究思路,请探究:当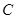 、
、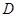 在线段
在线段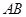 的异侧时的情形.
的异侧时的情形.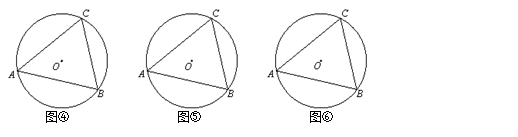
如图④,此时有 ,如图⑤,此时有 ,
如图⑥,此时有 .
由上面的探究,请用文字语言直接写出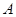 、
、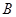 、
、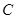 、
、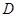 四点在同一个圆上的条件:
四点在同一个圆上的条件:
.
拓展延伸:(3)如何过圆上一点,仅用没有刻度的直尺,作出已知直径的垂线?
已知: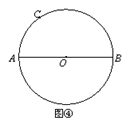 如图,
如图,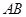 是⊙
是⊙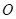 的直径,点
的直径,点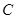 在⊙
在⊙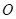 上,求作:
上,求作: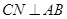 .
.
作法:①连接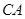 ,
,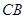 ;
;
②在 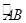 上任取异于
上任取异于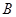 、
、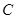 的一点
的一点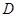 ,连接
,连接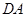 ,
,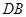 ;
;
③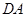 与
与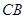 相交于
相交于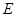 点,延长
点,延长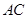 、
、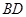 ,交于
,交于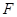 点;
点;
④连接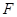 、
、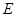 并延长,交直径
并延长,交直径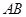 于
于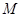 ;
;
⑤连接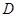 、
、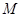 并延长,交⊙
并延长,交⊙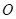 于N.连接
于N.连接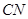 . 则
. 则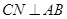 .
.
请按上述作法在图④中作图,并说明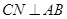 的理由.(提示:可以利用(2)中的结论)
的理由.(提示:可以利用(2)中的结论)
解方程:
(本小题满分10分)如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC。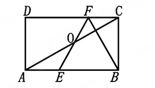
(1)求证:OE=OF;(2)若BC=2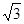 ,求AB的长。
,求AB的长。
(本小题满分10分)如图,一次函数y1=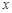 +1的图象与反比例函数
+1的图象与反比例函数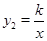 (k为常数,且k≠0)的图象都经过点A(m,2)。
(k为常数,且k≠0)的图象都经过点A(m,2)。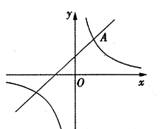
(1)求点A的坐标及反比例函数的表达式;
(2)结合图象直接比较:当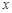 >0时,
>0时,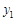 与
与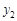 的大小。
的大小。
(本小题满分8分)新华商场销售某种空调,每台进货价为2500元。市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台。商场要想使这种空调的销售利润平均每天达到5000元,每台空调的定价应为多少元?
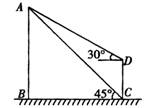
(本小题满分10分)如图,为了测量某风景区内一座塔AB的高度,某人分别在塔的对面一楼房CD的楼底C、楼顶D处,测得塔顶A的仰角为45°和30°,已知楼高CD为10m,求塔的高度。(结果精确到0.1m)(参考数据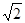 ≈1.41,
≈1.41,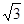 ≈1.73)
≈1.73)