（本小题12分）如图，直线
分别交轴于
、
，点
是该直线与反比例函数在第一象限内的一个交点，
轴于
，且
.
（1）求点的坐标；
（2）设点
与点在同一个反比例函数的图象上，且点在直线
的右侧，作
轴于
，当
与
相似时，求点的坐标.
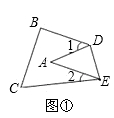
如图：将△ABC纸片沿DE折叠成图①，此时点A落在四边形BCDE内部，则∠A与∠1、∠2之间有一种数量关系保持不变，请找出这种数量关系并说明理由．
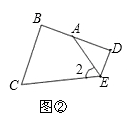
若折成图②或图③，即点A落在BE或CD上时，分别写出∠A与∠2；∠A与∠1之间的关系；（不必证明）
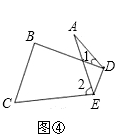
若折成图④，写出∠A与∠1、∠2之间的关系式；（不必证明）；若折成图⑤，写出∠A与∠1、∠2之间的关系式．（不必证明）
已知，如图在△ABC中，AD，AE分别是△ABC的高和角平分线若∠B=30°，∠C=50°，求∠DAE的度数；
若∠B=
，∠C=
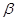，且
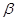＜，试写出∠DAE与
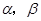有何关系？（不必证明）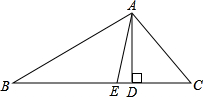
已知：如图，AD∥BE，∠1=∠2，试说明：∠A=∠E．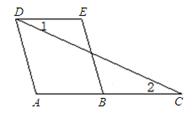
解方程组
时，一同学把c看错而得到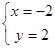
，而正确的解是
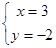，求a、b、c的值
如图，在方格纸内将△ABC经过一次平移后得到△A′B′C′，图中标出了点A的对应点A'．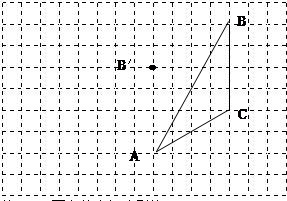
补全△A′B′C′根据下列条件，利用网格点和三角板画图：
画出AB边上的中线CD
画出BC边上的高线AE；
△A′B′C′的面积为．