在平面直角坐标系中,已知动点 ,点
,点 点
点 与点
与点 关于直线
关于直线 对称,且
对称,且 .直线
.直线 是过点
是过点 的任意一条直线.
的任意一条直线.
(1)求动点 所在曲线
所在曲线 的轨迹方程;
的轨迹方程;
(2)设直线 与曲线
与曲线 交于
交于 两点,且
两点,且 ,求直线
,求直线 的方程;
的方程;
(3)若直线 与曲线
与曲线 交于
交于 两点,与线段
两点,与线段 交于点
交于点 (点
(点 不同于点
不同于点 ),直线
),直线 与直线
与直线 交于点
交于点 ,求证:
,求证: 是定值.
是定值.
(本题满分12分)在直角坐标系中,已知椭圆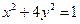 ,矩阵阵
,矩阵阵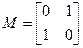 ,
,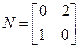 ,求在矩阵
,求在矩阵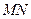 作用下变换所得到的图形的面积.
作用下变换所得到的图形的面积.
设 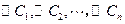 是圆心在抛物线
是圆心在抛物线  上的一系列圆,它们的圆心的横坐标分别记为
上的一系列圆,它们的圆心的横坐标分别记为  ,已知
,已知  ,又
,又 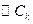
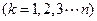 都与
都与 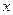 轴相切,且顺次逐个相邻外切.
轴相切,且顺次逐个相邻外切.
(1)求 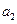 ;
;
(2)求由  构成的数列
构成的数列 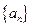 的通项公式;
的通项公式;
(3)求证: 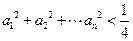 .
.
(
在锐角 中,
中,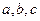 分别是角
分别是角 所对的边,且
所对的边,且
(1)确定角 的大小;
的大小;
(2)若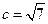 ,求
,求 面积的最大值.
面积的最大值.
已知某品牌汽车,购车费用是10万元,每年使用的保险费,养路费,汽油费约为 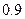 万元,汽车的维修费是第一年
万元,汽车的维修费是第一年 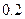 万元,以后逐年递增
万元,以后逐年递增 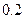 万元,问该品牌汽车使用多少年时,它的年平均费用最少?
万元,问该品牌汽车使用多少年时,它的年平均费用最少?
已知函数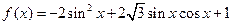 ,求
,求
(1)求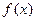 的最小正周期及对称中心;
的最小正周期及对称中心;
(2)当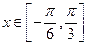 时,求
时,求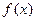 的最大值和最小值.
的最大值和最小值.