定义:若各项为正实数的数列 满足
满足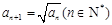 ,则称数列
,则称数列 为“算术平方根递推数列”.
为“算术平方根递推数列”.
已知数列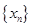 满足
满足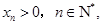 且
且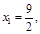 点
点 在二次函数
在二次函数 的图像上.
的图像上.
(1)试判断数列
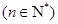 是否为算术平方根递推数列?若是,请说明你的理由;
是否为算术平方根递推数列?若是,请说明你的理由;
(2)记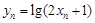
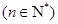 ,求证:数列
,求证:数列 是等比数列,并求出通项公式
是等比数列,并求出通项公式 ;
;
(3)从数列 中依据某种顺序自左至右取出其中的项
中依据某种顺序自左至右取出其中的项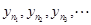 ,把这些项重新组成一个新数列
,把这些项重新组成一个新数列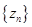 :
: .若数列
.若数列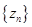 是首项为
是首项为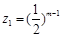 ,公比为
,公比为 的无穷等比数列,且数列
的无穷等比数列,且数列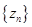 各项的和为
各项的和为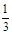 ,求正整数
,求正整数 的值.
的值.
已知函数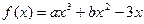 在
在 处取得极值。
处取得极值。
(1)讨论 和
和 是函数
是函数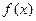 的极大值还是极小值;
的极大值还是极小值;
(2)过点 作曲线
作曲线 的切线,求此切线方程。
的切线,求此切线方程。
已知 的图象经过点
的图象经过点 ,且在
,且在 处的切线方程是
处的切线方程是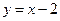
(1)求 的解析式;
的解析式;
(2)求 的单调递增区间
的单调递增区间
(1)已知椭圆的焦点为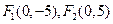 ,点
,点 在椭圆上,求它的方程(2)已知双曲线顶点间的距离为6,渐近线方程为
在椭圆上,求它的方程(2)已知双曲线顶点间的距离为6,渐近线方程为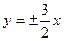 ,求它的方程.
,求它的方程.
求下列函数的导函数:
(1)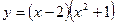
(2)
选作题,请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所做的第一题记分,每道题满分10分)
22、选修4—1:几何证明选讲
如图,△ABC的角平分线AD的延长线交于的外按圆于点E。
(I)证明:△ABC∽△ADC
(II)若△ABC的面积为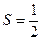 AD·AE,求∠BAC的大小。
AD·AE,求∠BAC的大小。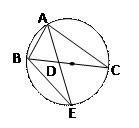
23、选修4—4:坐标系与参数方程
已知半圆C的参数方程
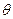 为参数且(0≤
为参数且(0≤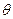 ≤
≤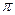 )
)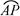 P为半圆C上一点,A(1,0)O为坐标原点,点M在射线OP上,线段OM与的长度均为
P为半圆C上一点,A(1,0)O为坐标原点,点M在射线OP上,线段OM与的长度均为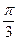 。
。
(I)求以O为极点, 轴为正半轴为极轴建立极坐标系求点M的极坐标。
轴为正半轴为极轴建立极坐标系求点M的极坐标。
(II)求直线AM的参数方程。
24、选修4—5,不等式选讲
已知函数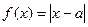

(I)若不等式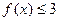 的解集为
的解集为 求a值。
求a值。
(II)在(I) 条件下,若 对一切实数
对一切实数 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。