(本小题满分12分)已知数列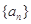 的前
的前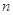 项和为
项和为 ,且
,且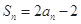 ;数列
;数列 满足
满足 ,
,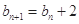 .
. .
.
(Ⅰ)求数列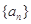 ,
, 的通项公式;
的通项公式;
(Ⅱ)记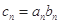 ,
, .求数列
.求数列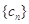 的前
的前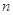 项和
项和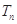 .
.
已知函数

(1)讨论函数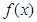 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(2)若函数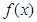 在
在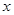 =1处取得极值,对任意的
=1处取得极值,对任意的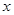 ∈(0,+∞),
∈(0,+∞),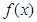 ≥
≥ 恒成立,求实数b的取值范围;
恒成立,求实数b的取值范围;
(3)当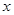 >
>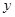 >
> 时,求证:
时,求证: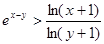
已知数列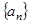 的前n项和为
的前n项和为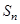 ,
,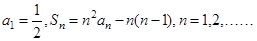
(1)证明:数列 是等差数列,并求
是等差数列,并求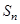 ;
;
(2)设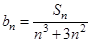 ,求证:
,求证: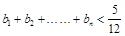 .
.
已知数列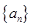 的前n项和为
的前n项和为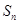 ,且
,且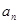 是
是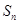 与2的等差中项,而数列
与2的等差中项,而数列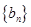 的首项为1,
的首项为1, .[来
.[来
(1)求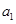 和
和 的值;
的值;
(2)求数列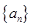 ,
,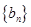 的通项
的通项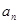 和
和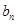 ;
;
(3)设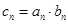 ,求数列
,求数列 的前n项和
的前n项和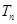 .
.
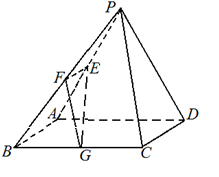
已知在四棱锥 中,底面
中,底面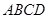 是边长为4的正方形,
是边长为4的正方形,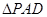 是正三角形,平面
是正三角形,平面 平面
平面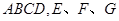 分别是
分别是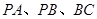 的中点.[Zx(1)求证:
的中点.[Zx(1)求证: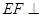 平面
平面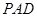 ;
;
(2)求平面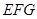 与平面
与平面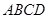 所成锐二面角的大小;
所成锐二面角的大小;
(3)若 为线段
为线段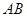 上靠近
上靠近 的一个动点,问当
的一个动点,问当 长度等于多少时,直线
长度等于多少时,直线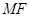 与平面
与平面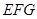 所成角的正弦值等于
所成角的正弦值等于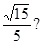
为推进成都市教育均衡发展,某中学需进一步壮大教师队伍,拟准备招聘一批优秀大学生到本单位就业,但在签约前要对他们的师范生素质进行测试。在待测试的某一个小组中有男、女生共10人(其中女生人数多于男生人数),如果从中随机选2人参加测试,其中恰为一男一女的概率为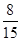 。(1)求该小组中女生的人数;(2)假设此项专业技能测试对该小组的学生而言,每个女生通过的概率均为
。(1)求该小组中女生的人数;(2)假设此项专业技能测试对该小组的学生而言,每个女生通过的概率均为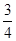 ,每个男生通过的概率均为
,每个男生通过的概率均为 。现对该小组中男生甲.男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量
。现对该小组中男生甲.男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量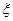 ,求
,求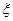 的分布列和数学期望.
的分布列和数学期望.