为推进成都市教育均衡发展，某中学需进一步壮大教师队伍，拟准备招聘一批优秀大学生到本单位就业，但在签约前要对他们的师范生素质进行测试。在待测试的某一个小组中有男、女生共10人（其中女生人数多于男生人数），如果从中随机选2人参加测试，其中恰为一男一女的概率为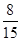
。（1）求该小组中女生的人数；（2）假设此项专业技能测试对该小组的学生而言，每个女生通过的概率均为
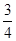，每个男生通过的概率均为
。现对该小组中男生甲．男生乙和女生丙3个人进行测试，记这3人中通过测试的人数为随机变量
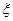，求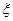的分布列和数学期望．
求双曲线
的实半轴长，虚半轴长，焦点坐标，离心率，渐近线方程。
已知函数
（1）求函数
的极值点；
（2）若直线
过点（0，—1），并且与曲线
相切，求直线的方程；
（3）设函数
，其中
，求函数
在
上的最小值.
（其中e为自然对数的底数）
已知椭圆
＞b＞
的离心率为
且椭圆的一个焦点与抛物线
的焦点重合，斜率为
的直线
过椭圆的上焦点且与椭圆相交于P，Q两点，线段PQ的垂直平分线与y轴相交于点M（0，m）.
（1）求椭圆的标准方程；
（2）求m的取值范围；
（3）试用m表示△MPQ的面积S，并求面积S的最大值.
直三棱柱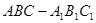
中，
，
，
，
，点D在
上．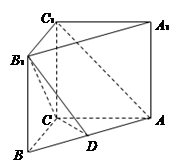 
（1）求证：
；
（2）若D是AB中点，求证：AC1∥平面B1CD；
（3）当
时，求二面角
的余弦值．
已知数列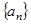
的前n项和为
，
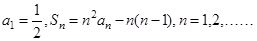
（1）证明：数列
是等差数列，并求；
（2）设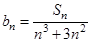
，求证：
.