对正整数,记,.
(1)求集合中元素的个数;
(2)若的子集中任意两个元素之和不是整数的平方,则称为"稀疏集".求的最大值,使能分成两个不相交的稀疏集的并集.
(本小题满分12分)已知函数
(1)求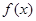 的单调递减区间;
的单调递减区间;
(2)求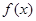 在区间[
在区间[ ]上的最大值和最小值并写出相应的
]上的最大值和最小值并写出相应的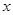 值.
值.
(本小题满分12分)已知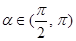 ,且
,且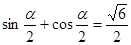 ,
,
(1)求 的值;
的值;
(2)若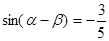 ,
,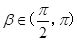 ,求
,求 的值.
的值.
(本小题满分10分)一船自西向东匀速航行。上午10时到达一灯塔P的南偏西750且距灯塔68海里的A处,下午2时到达灯塔P的东南方向B处,求这船的航行速度.
(本小题满分10分)选修4-5;不等式选讲
已知函数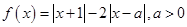 .
.
(Ⅰ)当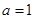 时求不等式
时求不等式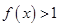 的解集;
的解集;
(Ⅱ)若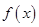 图像与
图像与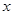 轴围成的三角形面积大于6,求a的取值范围.
轴围成的三角形面积大于6,求a的取值范围.
(本小题满分10分)选修4-4:坐标系与参数方程
已知在平面直角坐标系 中,直线
中,直线 的参数方程是
的参数方程是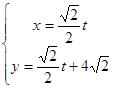 (
( 是参数),以原点
是参数),以原点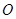 为极点,
为极点, 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程
的极坐标方程 .
.
(Ⅰ)判断直线 与曲线
与曲线 的位置关系;
的位置关系;
(Ⅱ)设 为曲线
为曲线 上任意一点,求
上任意一点,求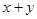 的取值范围.
的取值范围.