(本小题满分14分)已知函数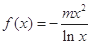 ,
, ,其中
,其中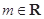 且
且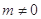 .
. 为自然对数的底数.
为自然对数的底数.
(Ⅰ)当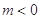 时,求函数
时,求函数 的单调区间和极小值;
的单调区间和极小值;
(Ⅱ)当 时,若函数
时,若函数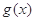 存在
存在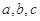 三个零点,且
三个零点,且 ,试证明:
,试证明: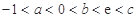 ;
;
(Ⅲ)是否存在负数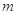 ,对
,对 ,
,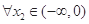 ,都有
,都有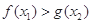 成立?若存在,求出
成立?若存在,求出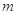 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
甲、乙两人参加一次英语口语考试,已知在备选的10道试题中,甲能答对其中的6题,乙能答对其中的8题.规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才算合格.
(Ⅰ)求甲、乙两人考试均合格的概率;
(Ⅱ)求甲答对试题数 的概率分布.
的概率分布.
某研究机构准备举办一次数学新课程研讨会,共邀请50名一线教师参加,使用不同版本教材的教师人数如下表所示
| 版本 |
人教A版 |
人教B版 |
苏教版 |
北师大版 |
| 人数 |
20 |
15 |
5 |
10 |
(1)从这50名教师中随机选出2名,问这2人使用相同版本教材的概率是多少?
(2)若随机选出的2名教师都使用人教版教材,现设使用人教A版教材的教师人数为 ,求随机变量
,求随机变量 的分布列
的分布列
甲、乙二射击运动员分别对一目标射击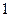 次,甲射中的概率为
次,甲射中的概率为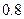 ,乙射中的概率为
,乙射中的概率为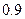 ,求:
,求:
(1) 人都射中目标的概率;
人都射中目标的概率;
(2) 人中恰有
人中恰有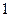 人射中目标的概率;
人射中目标的概率;
(3) 人至少有
人至少有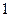 人射中目标的概率;
人射中目标的概率;
(4) 人至多有
人至多有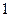 人射中目标的概率?
人射中目标的概率?
某商场准备在国庆节期间举行促销活动,根据市场调查,该商场决定从2种服装商品,2种家电商品,3种日用商品中,选出3种商品进行促销活动.
(Ⅰ)试求选出的3种商品中至少有一种是日用商品的概率;
(Ⅱ)商场对选出的某商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高150元,同时,若顾客购买该商品,则允许有3次抽奖的机会,若中奖,则每次中奖都获得数额为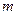 的奖金.假设顾客每次抽奖时获奖与否的概率都是
的奖金.假设顾客每次抽奖时获奖与否的概率都是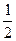 ,请问:商场应将每次中奖奖金数额
,请问:商场应将每次中奖奖金数额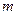 最高定为多少元,才能使促销方案对商场有利?
最高定为多少元,才能使促销方案对商场有利?
甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设每人面试合格的概率都是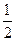 ,且面试是否合格互不影响.求:至少有1人面试合格的概率;
,且面试是否合格互不影响.求:至少有1人面试合格的概率;